题目内容
8.下列命题是真命题的有④⑤①平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆;
②如果向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是三个不共线的向量,$\overrightarrow{a}$是空间任一向量,那么存在唯一一组实数λ1,λ2,λ3使得$\overrightarrow{a}$=λ1$\overrightarrow{{e}_{1}}$+λ2$\overrightarrow{{e}_{2}}$+λ3$\overrightarrow{{e}_{3}}$;
③方程y=$\sqrt{x}$与x=y2表示同一曲线;
④若命题p是命题q的充分非必要条件,则¬p是¬q的必要非充分条件;
⑤方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{2-m}$=1表示双曲线的充要条件是2<m<5.
分析 ①,当常数大于F1,F2的距离时轨迹是椭圆;
②,三个不共线的向量,不一定不共面,它们不一定能作为空间基底;
③,方程y=$\sqrt{x}$与x=y2中x的取值范围不一样,不表示同一曲线;
④,若命题p是命题q的充分非必要条件,则¬q是¬p的充分非必要条件,则¬p是¬q的必要非充分条件;
⑤,方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{2-m}$=1表示双曲线的充要条件是(5-m)(2-m)<0⇒2<m<5.
解答 解:对于①,平面内与两个定点F1,F2的距离之和等于常数,当常数大于F1,F2的距离时轨迹是椭圆,故错;
对于②,向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是三个不共线的向量,不一定不共面,故它们不一定能作为空间基底,故错;
对于 ③,方程y=$\sqrt{x}$与x=y2中x的取值范围不一样,不表示同一曲线,故错;
对于④,若命题p是命题q的充分非必要条件,则¬q是¬p的充分非必要条件,则¬p是¬q的必要非充分条件,正确;
对于⑤,方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{2-m}$=1表示双曲线的充要条件是(5-m)(2-m)<0⇒2<m<5.故正确.
故答案为:④⑤
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
相关题目
6.执行如图的程序框图,若输入k的值为3,则输出S的值为( )
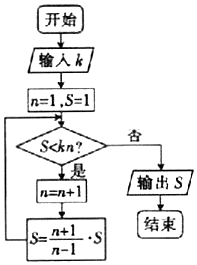

| A. | 10 | B. | 15 | C. | 18 | D. | 21 |
17.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{{x}^{2}}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=x3,g(x)=$\root{9}{{x}^{9}}$ |
 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.