题目内容

（Ⅰ）已知tanα=
1
4
，则cos2α+sin2α的值为
 
．
（Ⅱ）已知α是三角形的内角，且sinα+cosα=
1
5
．
（1）求tanα的值；
（2）把
1
cos2α-sin2α
用tanα表示出来，并求其值．
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：（Ⅰ）运用二倍角公式以及同角的平方关系和商数关系，注意添分母1，再由弦化切，即可得到；
（Ⅱ）（1）运用同角的平方关系和商数关系，计算即可得到；
（2）运用二倍角公式以及同角的平方关系和商数关系，计算即可得到所求值．
解答： 解：（Ⅰ）cos2α+sin2α=cos2α-sin2α+sin2α=cos2α
=
cos2α
cos2α+sin2α
=
1
1+tan2α
=
1
1+
1
16
=
16
17
；
故答案为：
16
17

（Ⅱ）（1）sinα+cosα=
1
5
，平方可得1+2sinαcosα=
1
25
，
sinαcosα=-
12
25
＜0，
由α是三角形的内角，则sinα＞0，cosα＜0，
sinα-cosα=
(sinα-cosα)2
=
1-2sinαcosα
=
1+
24
25
=
7
5
，
解得sinα=
4
5
，cosα=-
3
5
，
则tanα=
sinα
cosα
=-
4
3
；
（2）
1
cos2α-sin2α
=
sin2α+cos2α
cos2α-sin2α-2sinαcosα

=
tan2α+1
1-tan2α-2tanα

=
(-
4
3
)2+1
1-(-
4
3
)2-2×(-
4
3
)
=
25
17
..
点评：本题考查二倍角公式和同角的平方关系及商数关系的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
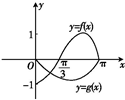已知y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域均为[-π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式
f(x)
g(x)
＜0的解集为（　　）
A、（-
2π
3
，
π
3
）
B、（
π
3
，π）
C、（-
2π
3
，
π
3
）∪（
π
3
，π）
D、（-
π
3
，0）∪（
π
3
，π）
学校要安排一场文艺玩会的11个节目的出场顺序，除第1个节目和最后1个节目已确定外，4个音乐节目要求排在第2、5、7、10的位置，3个舞蹈节目要求排在第3、6、9的位置，2个曲艺节目要求排在第4、8位置，共有多少种不同的排法？
已知命题p：对于函数f（x）=x3+ax2+bx+c（a，b，c∈R），若f′（x0）=0，则x0是f（x）的一个极值点．则命题p的逆命题、否命题、逆否命题中，正确命题的个数为
 
．
已知sin2a+sina+b=0方程有解，求b的取值范围．
已知数列{an}为等比数列，且a3a9=2a52，a2=2，则a1等于（　　）
A、±
2
B、
2
C、-
2
D、2
对于函数f（x），若存在区间M=[a，b]，使得{y|y=f（x），x∈M}=M，则称区间M为函数f（x）的一个“稳定区间”．给出下列函数：
①f（x）=x；      
②f（x）=ex；
③f（x）=sinx；   
④f（x）=ln（x+1）．
其中存在“稳定区间”的函数的个数有（　　）
A、1B、2C、3D、4
已知实数x，y满足
lg(x-y+4)
lg(3x+y-4)
≥1，则
x-y+4
3x+y-4
的取值范围
 
．
已知点A是曲线y=
3
ln x（x≥1）上的动点，在点A处的切线倾斜角为θ，则θ的取值范围是（　　）
A、[0，
π
2
]
B、[0，
π
3
]
C、（0，
π
3
]
D、[
π
3
，
π
2
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网