题目内容
已知两个命题r(x):sin x+cos x>m,s(x):x2+mx+1>0.如果对∀x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
解 ∵sin x+cos x= sin
sin ≥-
≥- ,∴当r(x)是真命题时,m<-
,∴当r(x)是真命题时,m<- .又∵对∀x∈R,当s(x)为真命题时,
.又∵对∀x∈R,当s(x)为真命题时,
即x2+mx+1>0恒成立有Δ=m2-4<0,∴-2<m<2.
∴当r(x)为真,s(x)为假时,m<- ,同时m≤-2或m≥2,即m≤-2.当r(x)为假,s(x)为真时,m≥-
,同时m≤-2或m≥2,即m≤-2.当r(x)为假,s(x)为真时,m≥- 且-2<m<2,即-
且-2<m<2,即- ≤m<2.
≤m<2.
综上,实数m的取值范围是m≤-2或- ≤m<2.
≤m<2.

练习册系列答案
相关题目
 a∈(0,+∞),
a∈(0,+∞), θ∈R,使asinθ≥a成立,则cos(θ-
θ∈R,使asinθ≥a成立,则cos(θ- )的值为 .
)的值为 . ,3],则函数F(x)=f(x)+
,3],则函数F(x)=f(x)+ 的值域是( )
的值域是( ) ]
] ,
, 则f(f(-2))=________.
则f(f(-2))=________.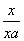 (x≠a).
(x≠a). 是R上的单调减函数,则实数a的取值范围是( )
是R上的单调减函数,则实数a的取值范围是( ) ]
]