题目内容
已知p：方程x2＋mx＋1＝0有两个不等的负根；q：方程4x2＋4(m－2)x＋1＝0无实根．若p或q为真，p且q为假，求m的取值范围．
解：若方程x2＋mx＋1＝0有两不等的负根，
则
解得m＞2，即p：m＞2 ............3分
若方程4x2＋4(m－2)x＋1＝0无实根，则Δ＝16(m－2)2－16＝16(m2－4m＋3)＜0，
解得1＜m＜3，即q：1＜m＜3. ...........6分
因p或q为真，所以p，q至少有一为真，
又p且q为假，所以p、q至少有一为假，因此，p、q两命题应一真一假，
即p为真，q为假或p为假，q为真． ...........8分
∴
或
...........10分
解得m≥3或1＜m≤2. ...............12分
练习册系列答案
名校课堂系列答案
相关题目
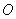，焦点为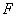
，
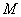是抛物线上的动点，则
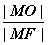的最大值为 ．
、
、
成等比数列，且
，若
，
为正常数，则
B．
C．
D．
则
是
的 ( )
，则目标函数z=x+2y的最小值为＿＿＿＿＿＿＿＿ 
中，若
，
，则
的值为 （ ）
B．
C．
D．
