题目内容
2.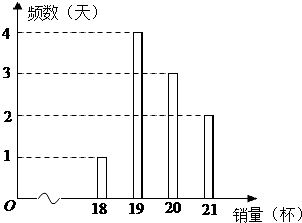 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:设x为每天饮品的销量,y为该店每天的利润.
(1)求y关于x的表达式;
(2)从日利润不少于96元的几天里任选2天,求选出的这2天日利润都是97元的概率.
分析 (1)利用频率分布直方图,列出函数的关系式即可.
(2)求出销量为20杯的有3天,记为a,b,c,销量为21杯的有2天,记为A,B,从这5天中任取2天,列出事件情况,求解概率即可.
解答 解:(1)$y=\left\{\begin{array}{l}(8-3)x=5x(x≤19)\\(8-3)×19+(4-3)×(x-19)=76+x(x>19).\end{array}\right.$
(2)由(1)可知:日销售量不少于20杯时,日利润不少于96元,日销售量为21杯时,日利润为97元,从条形图可以看出,销量为20杯的有3天,记为a,b,c,销量为21杯的有2天,记为A,B,从这5天中任取2天,包括(a,b),(a,c),(a,A),(a,B),(b,c),(b,A),(b,B),(c,A),(c,B),(A,B),共10种情况,
其中选出的2天销量都为21天的情况只有1种,故其概率为$\frac{1}{10}$.
点评 本题考查频率分布直方图的应用,函数的解析式的求法,概率的求法,考查计算能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
11.定义在(-2,2)上的偶函数f(x),当x≥0时,f(x)为减函数,若f(m-1)<f(-m),则实数m的取值范围是( )
| A. | $({-1,\frac{1}{2}})$ | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},2})$ | D. | $[{-1,\frac{1}{2}})$ |
7.口袋中放有大小相等的2个红球和1个白球,有放回地每次摸取1个球,定义数列{an}:若第n次摸到红球,an=-1;若第n次摸到白球,an=1.如果Sn为数列{an}的前n项和,那么S7=3的概率为( )
| A. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | B. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{1}{3}})^5}$ | C. | $C_7^3×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | D. | $C_7^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^5}$ |
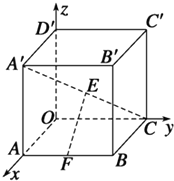 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.