题目内容
1．在△ABC中，角A．B、C的对边分别为a，b，c，若2a=3b，则$\frac{9si{n}^{2}B-si{n}^{2}A}{si{n}^{2}A}$=（ ）| A． | 2 | B． | 3 | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
分析 由已知条件2a=3b，结合正弦定理推知3sinB=2sinA，故sinA=$\frac{3}{2}$sinB，将其代入所求的代数式进行求值即可．
解答 解：∵在△ABC中，角A．B、C的对边分别为a，b，c，2a=3b，
∴由正弦定理得到：3sinB=2sinA，故sinA=$\frac{3}{2}$sinB，
∴$\frac{9si{n}^{2}B-si{n}^{2}A}{si{n}^{2}A}$=$\frac{9si{n}^{2}B-\frac{9}{4}si{n}^{2}B}{\frac{9}{4}si{n}^{2}B}$=3．
故选：B．
点评 本题考查三角形的正弦定理的运用，考查运算能力，属于中档题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
10．下列各组函数中，表示同一函数的是（ ）
| A． | y=1，y=x0 | B． | $y=x\;，\;y=\root{3}{x^3}$ | ||
| C． | $y=\sqrt{x-1}•\sqrt{x+1}\;，\;y=\sqrt{{x^2}-1}$ | D． | $y=|x|\;，\;y={（\sqrt{x}）^2}$ |
11．定义在（-2，2）上的偶函数f（x），当x≥0时，f（x）为减函数，若f（m-1）＜f（-m），则实数m的取值范围是（ ）
| A． | $（{-1，\frac{1}{2}}）$ | B． | $（{-∞，\frac{1}{2}}）$ | C． | $（{\frac{1}{2}，2}）$ | D． | $[{-1，\frac{1}{2}}）$ |
15．已知x5=-243，那么x=（ ）
| A． | 3 | B． | -3 | C． | -3或3 | D． | 不存在 |
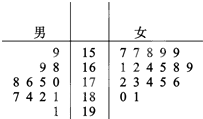某部队为了在大阅兵中树立军队的良好形象，决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员，这30名军人的身高如图：单位：cm
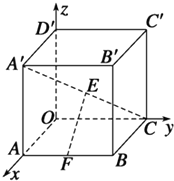如图所示，在空间直角坐标系中，有一棱长为a的正方体ABCO-A′B′C′D′，A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$．