题目内容
3.(Ⅰ)求612,840的最大公约数;(Ⅱ)已知f(x)=3x6+5x5+6x4+79x3-8x2+35x+12,用秦九韶算法计算:当x=-4时v3的值.
分析 (Ⅰ)用辗转消除法求612,840的最大公约数;
(Ⅱ)由于多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6=(((((3x+5)x+6)x+79)x-8)x+35)x+12,可得当x=-4时,v0=3,v1=3×(-4)+5=-7,v2,v3即可得出.
解答 解:(Ⅰ)840=612+228,612=2×228+156,228=156+72,156+2×72+12,72=6×12,…(5分)
所以612,840的最大公约数为12; …(6分)
(Ⅱ)∵多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6
=(((((3x+5)x+6)x+79)x-8)x+35)x+12,
当x=-4时,
∴v0=3,v1=3×(-4)+5=-7,v2=-7×(-4)+6=34,v3=34×(-4)+79=-57..…(12分)
点评 本题考查辗转消除法,考查了秦九韶算法计算多项式的值,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.“对任意x∈(0,$\frac{π}{2}$),ksin$\frac{x}{2}$cos$\frac{x}{2}$>ln(x+1)”是“k≥2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.已知集合A={a-2,2a2+5a,12},-3∈A,则a的值为( )
| A. | -1 | B. | $-\frac{3}{2}$ | C. | $-1或-\frac{3}{2}$ | D. | $-1或-\frac{3}{2}$ |
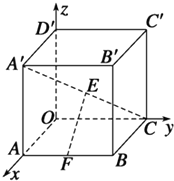 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.