题目内容

“|x-A|＜
?
2
，且|y-A|＜
?
2
”是“|x-y|＜?”（x，y，A，?∈R）的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：“|x-A|＜
?
2
，且|y-A|＜
?
2
”⇒|x-y|=|（x-A）-（y-A）|≤|x-A|+|y-A|＜?，反之不成立．即可判断出．
解答： 解：“|x-A|＜
?
2
，且|y-A|＜
?
2
”⇒|x-y|=|（x-A）-（y-A）|≤|x-A|+|y-A|＜?，
反之不成立．
∴“|x-A|＜
?
2
，且|y-A|＜
?
2
”是“|x-y|＜?”充分非必要条件．
故选：A．
点评：判断充要条件的方法是：
①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；
②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；
③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；
④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．
⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
练习册系列答案
相关题目
二项式（1+x）n展开式的二项式系数之和为64，则（1-2x）n展开式第四项的系数为（　　）
A、20B、-160
C、160D、-20
若集合A={-1，-2}，B={0，1}，则集合C={z|z=y-x，x∈A，y∈B}所有子集的个数为（　　）
A、2B、4C、8D、16
设全集U=R，集合M={x|x＞1或x＜-1}，N={x|0＜x＜2}，则∁U（M∪N）=（　　）
A、{x|-1≤x≤1}
B、{x|0＜x≤1}
C、{x|-1≤x≤0}
D、{x|x＜1}
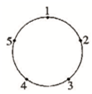如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙按顺时针方向绕圆从一个点跳到另一点；若停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次可以跳两个点，该青蛙从5这点跳起，跳2008次后它将停在的点是（　　）
A、1B、2C、3D、4
某酒厂制作了3种不同的精美卡片，每瓶酒酒盒随机装入一张卡片，集齐3种卡片可获奖，现购买该种酒5瓶，能获奖的概率为（　　）
A、
31
81
B、
33
81
C、
48
81
D、
50
81
集合P={（x，y）|y=k}，Q={（x，y）|y=ax+1，a＞0，a≠1}，已知P∩Q只有一个子集，那么实数k的取值范围是（　　）
A、（-∞，1）
B、（-∞，1]
C、（1，+∞）
D、（-∞，+∞）
下列命题正确的个数是（　　）
①“在三角形ABC中，若sinA＞sinB，则A＞B”的否命题是真命题；
②命题p：x≠2或y≠3，命题q：x+y≠5则p是q的必要不充分条件；
③“?x∈R，x3-x2+1≤0”的否定是“?x∈R，x3-x2+1＞0”．
A、0B、1C、2D、3
若
OA
=
a
，
OB
=
b
，则∠AOB的平分线上的向量
OC
为（　　）
A、
a
|
a
|
+
b
|
b
|
B、
|
b
|
a
+|
a
|
b
|
a
|+|
b
|
C、λ（
a
|
a
|
+
b
|
b
|
），λ由
DC
确定
D、
a
+
b
|
a
+
b
|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网