题目内容
1.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=2$\sqrt{3}$$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$=( )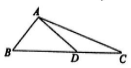
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -2$\sqrt{3}$ |
分析 由题意利用两个向量垂直的性质、两个向量的加减法的法则,以及其几何意义,把要求的式子化为2$\sqrt{3}$${\overrightarrow{AD}}^{2}$-2$\sqrt{3}$$\overrightarrow{AB}•\overrightarrow{AD}$,计算求的结果.
解答 解:在△ABC中,AD⊥AB,$\overrightarrow{BC}$=2$\sqrt{3}$$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,
则$\overrightarrow{AC}$•$\overrightarrow{AD}$=($\overrightarrow{AB}$+$\overrightarrow{BC}$)•$\overrightarrow{AD}$=$\overrightarrow{AB}•\overrightarrow{AD}$+$\overrightarrow{BC}•\overrightarrow{AD}$=$\overrightarrow{BC}•\overrightarrow{AD}$
=0+2$\sqrt{3}$$\overrightarrow{BD}$•$\overrightarrow{AD}$=2$\sqrt{3}$($\overrightarrow{AD}$-$\overrightarrow{AB}$)•$\overrightarrow{AD}$
=2$\sqrt{3}$${\overrightarrow{AD}}^{2}$-2$\sqrt{3}$$\overrightarrow{AB}•\overrightarrow{AD}$=2$\sqrt{3}$•1-0=2$\sqrt{3}$,
故选:A.
点评 本题考查了平面向量数量积的运算,两条直线直线垂直,则两直线上的向量也垂直,等价于两向量的数量积为0,解题中还运用了向量的模的性质,属于中档题.

| A. | 3 | B. | $\sqrt{3}$ | C. | -3 | D. | -$\sqrt{3}$ |
| A. | {1,4,6} | B. | {2,4,6} | C. | {2,4} | D. | {4} |
| A. | ¬p:存在x∈R,sinx≥1 | B. | ¬p:任意x∈R,sinx≥1 | ||
| C. | ¬p:存在x∈R,sinx>1 | D. | ¬p:任意x∈R,sinx>1 |