题目内容
10.已知命题p:任意x∈R,sinx≤1,则( )| A. | ¬p:存在x∈R,sinx≥1 | B. | ¬p:任意x∈R,sinx≥1 | ||
| C. | ¬p:存在x∈R,sinx>1 | D. | ¬p:任意x∈R,sinx>1 |
分析 根据全称命题的否定是特称命题进行判断即可.
解答 解:命题是全称命题,则命题的否定是特称命题,
即存在x∈R,sinx>1,
故选:C
点评 本题主要考查含有量词的命题的否定,根据全称命题的否定是特称命题是解决本题的关键.

练习册系列答案
相关题目
1.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=2$\sqrt{3}$$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$=( )
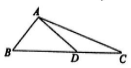

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -2$\sqrt{3}$ |
18.命题“|x|+|y|≠0”是命题“x≠0或y≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.函数$y=\frac{lnx}{x}$的导数为( )
| A. | $y=\frac{1-lnx}{x^2}$ | B. | $y=\frac{1+lnx}{x^2}$ | C. | $y=\frac{lnx-1}{x^2}$ | D. | $y=\frac{x+lnx}{x^2}$ |
20.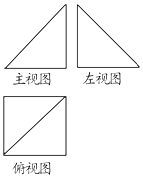 如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
 如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
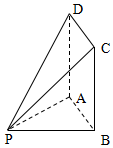 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.