题目内容
9.已知△ABC的外接圆的圆心为O,半径为2,且$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,则向量$\overrightarrow{CA}$在向量$\overrightarrow{CB}$方向上的投影为( )| A. | 3 | B. | $\sqrt{3}$ | C. | -3 | D. | -$\sqrt{3}$ |
分析 由题意可得四边形OBAC是边长为2的菱形,且∠ABO=∠ACO=60°,∠ACB=$\frac{1}{2}$∠ACO=30°,可得向量$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为:|$\overrightarrow{AC}$|•cos∠ACB,计算求的结果.
解答 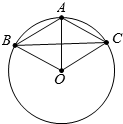 解:△ABC的外接圆的圆心为O,半径为2,且$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,∴$\overrightarrow{OB}$=$\overrightarrow{CA}$,
解:△ABC的外接圆的圆心为O,半径为2,且$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,∴$\overrightarrow{OB}$=$\overrightarrow{CA}$,
∴OBAC为平行四边形.
∵△ABC的外接圆的圆心为O,半径为2,得|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{OB}$|,
∴四边形OBAC是边长为2的菱形,且∠ABO=∠ACO=60°,
因此,∠ACB=$\frac{1}{2}$∠ACO=30°,
∴向量$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为:|$\overrightarrow{AC}$|•cos∠ACB=2cos30°=$\sqrt{3}$,
故选:B.
点评 本题给出三角形外接圆满足的向量等式,求向量的投影,着重考查了向量的加法法则、向量数量积的运算性质和向量在几何中的应用等知识,属于中档题.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
1.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=2$\sqrt{3}$$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$=( )
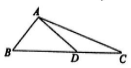

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -2$\sqrt{3}$ |
18.命题“|x|+|y|≠0”是命题“x≠0或y≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
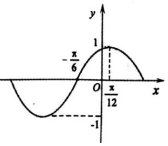 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.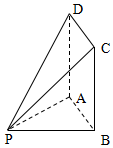 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.