题目内容
7.函数f(x)=2${\;}^{\frac{1}{2}-x}$的大致图象为( )| A. | 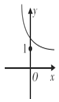 | B. | 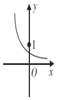 | C. | 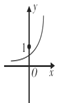 | D. | 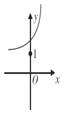 |
分析 将解析式变形为f(x)=$(\frac{1}{2})^{x-\frac{1}{2}}$,根据指数函数的图象进行选择.
解答 解:解析式变形为f(x)=$(\frac{1}{2})^{x-\frac{1}{2}}$,0<$\frac{1}{2}$<1,
函数f(x)=2${\;}^{\frac{1}{2}-x}$的大致图象为函数y=$(\frac{1}{2})^{x}$向右平移$\frac{1}{2}$个单位得到的;
所以A正确;
故选A.
点评 本题考查了指数函数的图象以及图象的平移;属于基础题.

练习册系列答案
相关题目
18.给出下列四个函数,在(0,+∞)为增函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=(x-1)2 | C. | y=2-x | D. | y=log2(x+2) |
12.设集合A={1,2,3,5},B={2,4,6},则A∩B=( )
| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {4,6,7,8} |
19.若m,n满足m+n-1=0,则直线mx+y+n=0过定点( )
| A. | (1,-1) | B. | (0,-n) | C. | (0,0) | D. | (-1,1) |
17.已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上单调递增,若$\frac{{|f(lnx)-f(ln\frac{1}{x})|}}{2}>f(1)$,则x的取值范围是( )
| A. | $(-∞\;,\;\;\frac{1}{e})$ | B. | (e,+∞) | C. | $(\frac{1}{e}\;,\;\;e)$ | D. | $(0\;,\;\;\frac{1}{e})$∪(e,+∞) |
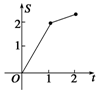
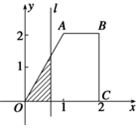 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )