题目内容
．在△ABC中，a，b，c分别是角A，B，C所对的边，设向量
=（a+b，c），
（b+c，a-b），且
∥
．
（1）求角A的大小；
（2）若B=
，a=3，求△ABC的面积．
| m |
| n |
| m |
| n |
（1）求角A的大小；
（2）若B=
| π |
| 6 |
考点：余弦定理,平行向量与共线向量
专题：解三角形
分析：（1）由两向量的坐标及两向量平行满足的条件列出关系式，再利用余弦定理表示出cosA，将得出关系式代入求出cosA的值，即可确定出A的度数；
（2）由a，sinB，sinA的值，利用正弦定理求出b的值，确定出C的度数，利用三角形面积公式求出三角形ABC面积即可．
（2）由a，sinB，sinA的值，利用正弦定理求出b的值，确定出C的度数，利用三角形面积公式求出三角形ABC面积即可．
解答：
解：（1）∵向量
=（a+b，c），
（b+c，a-b），且
∥
，
∴（a+b）（a-b）=c（b+c），即b2+c2-a2=-bc，
∴cosA=
=-
，
则A=
；
（2）∵B=
，a=3，A=
，
∴C=
，由正弦定理
=
得：b=
=
=
，
则S△ABC=
absinC=
．
| m |
| n |
| m |
| n |
∴（a+b）（a-b）=c（b+c），即b2+c2-a2=-bc，
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
则A=
| 2π |
| 3 |
（2）∵B=
| π |
| 6 |
| 2π |
| 3 |
∴C=
| π |
| 6 |
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
3×
| ||||
|
| 3 |
则S△ABC=
| 1 |
| 2 |
3
| ||
| 4 |
点评：此题考查了正弦、余弦定理，平面向量的数量积运算，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
各项为实数的等差数列的公差为4，其首项的平方与其余各项之和不超过100，这样的数列至多有（ ）项．
| A、5 | B、6 | C、7 | D、8 |
下列函数中，最小正周期为π的偶函数是（ ）
| A、y=sin2x | ||
B、y=cos
| ||
C、y=
| ||
| D、y=sin2x+cos2x |
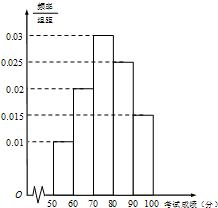某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．