题目内容
将一颗骰子先后抛掷2次,观察向上的点数,则点数之和是4的倍数的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:将一颗骰子先后抛掷2次,观察向上的点数,基本事件总数n=6×6=36,点数之和是4的倍数包含的基本事件的个数m=9,由此能求出点数之和是4的倍数的概率.
解答:
解:将一颗骰子先后抛掷2次,观察向上的点数,
基本事件总数n=6×6=36,
点数之和是4的倍数包含的基本事件的个数m=9,
∴点数之和是4的倍数的概率p=
=
.
故答案为:
.
基本事件总数n=6×6=36,
点数之和是4的倍数包含的基本事件的个数m=9,
∴点数之和是4的倍数的概率p=
| 9 |
| 36 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件的概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x2-2x-3≤0},B={0,1,2,3,4},则A∩B=( )
| A、{1,2,3} |
| B、{0,1,2,3} |
| C、{-1,0,1,2,3} |
| D、{0,1,2} |
已知函数y=f(x)的图象如图所示,则下列说法中错误的是( )
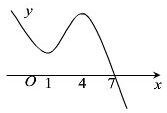

| A、f(x)在区间(-∞,1)上单调递减 |
| B、f(x)在区间(1,4)上单调递增 |
| C、当4<x<7时,f'(x)>0 |
| D、当x=1时,f'(x)=0 |