题目内容
19.已知实数a,b,c满足a,b,c∈R+.(Ⅰ)若ab=1,证明:($\frac{1}{a}$+$\frac{1}{b}$)2≥4;
(Ⅱ)若a+b+c=3,且$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤|2x-1|-|x-2|+3恒成立,求x的取值范围.
分析 (Ⅰ)利用基本不等式,即可证明结论;
(Ⅱ)($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤(1+1+1)(a+b+c)=9,$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤|2x-1|-|x-2|+3恒成立,可得9≤|2x-1|-|x-2|+3,分类讨论,即可求x的取值范围.
解答 (Ⅰ)证明:∵ab=1,∴($\frac{1}{a}$+$\frac{1}{b}$)2=a2+b2+2≥2ab+2=4;
(Ⅱ)解:($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤(1+1+1)(a+b+c)=9,
∵$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤|2x-1|-|x-2|+3恒成立,
∴9≤|2x-1|-|x-2|+3,
∴|2x-1|-|x-2|≥6,
x<$\frac{1}{2}$,不等式化为-2x+1+x-2≥6,∴x≤-7,∴x≤-7,
$\frac{1}{2}≤x≤2$,不等式化为2x-1+x-2≥6,∴x≥3,不成立;
x>2,不等式化为2x-1-x+2≥6,∴x≥5,∴x≥5;
综上所述,x≤-7或x≥5.
点评 本题考查不等式的证明,考查柯西不等式的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.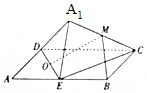 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 异面直线BM与A1E所成角是定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
4.在区间[0,1]内随机取两个数分别为a,b,则使得方程x2+2ax+b2=0有实根的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
8.已知各项均不相等的等比数列{an}中,a2=1,且$\frac{1}{4}$a1,a3,$\frac{7}{4}$a5成等差数列,则a4等于( )
| A. | $\frac{1}{49}$ | B. | 49 | C. | $\frac{1}{7}$ | D. | 7 |
 如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2$\sqrt{3}$,如图2.
如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2$\sqrt{3}$,如图2.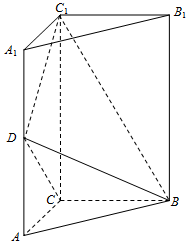 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠ACB=90°,AC=BC=1,AA1=2,D是棱AA1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠ACB=90°,AC=BC=1,AA1=2,D是棱AA1的中点.