题目内容
曲线y=x3+x2-1在点P（-1，-1）处的切线方程是 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出曲线y=x3+x2-1在点P（-1，-1）处的导数值，这个导数值即函数图象在该点处的切线的斜率，然后根据直线的点斜式方程求解即可．
解答：
解：因为y=x3+x2-1，
所以y′=3x2+2x，
曲线y=x3+x2-1在点P（-1，-1）处的切线的斜率为：y′|x=1=1．
此处的切线方程为：y+1=x+1，即y=x．
故答案为：y=x．
所以y′=3x2+2x，
曲线y=x3+x2-1在点P（-1，-1）处的切线的斜率为：y′|x=1=1．
此处的切线方程为：y+1=x+1，即y=x．
故答案为：y=x．
点评：本题考查导数的几何意义、关键是求出直线的斜率，正确利用直线的点斜式方程，考查计算能力．
练习册系列答案
相关题目
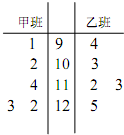为了解甲、乙两个班级某次考试的数学成绩，从甲、乙两个班级中分别随机抽取5名学生的成绩（单位：分）作样本，如图是样本的茎叶图：
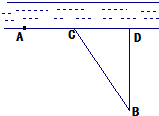甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40千米的B处，乙厂到河岸的垂足D与A相距50千米，两厂要在此岸边AD之间合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，若CD=x千米，设总的水管费用为y元，如图所示，
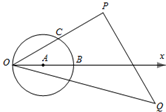如图，在极坐标系中，设极径为ρ（ρ＞0），极角为θ（0≤θ＜2π），⊙A的极坐标方程为ρ=2cosθ，点C在极轴的上方，∠AOC=