题目内容
16．
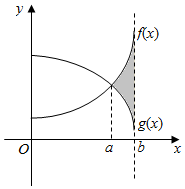如图所示，已知${∫}_{0}^{b}$f（x）dx=11，${∫}_{0}^{b}$g（x）dx=9，${∫}_{0}^{a}$[g（x）-f（x）]dx=5．则图中阴影部分的面积为7．
分析 根据定积分的几何意义解答．
解答 解：图中阴影部分的面积为S=${∫}_{a}^{b}$[f（x）-g（x）]dx=${∫}_{0}^{b}$f（x）dx-${∫}_{0}^{a}$f（x）dx-[${∫}_{0}^{b}$g（x）dx-${∫}_{0}^{a}$g（x）dx]，
=${∫}_{0}^{b}$f（x）dx-${∫}_{0}^{b}$g（x）dx+${∫}_{0}^{a}$[g（x）-f（x）]dx=11-9+5=7，
故答案为：7．
点评 本题考查定积分在求面积中的应用，属于基础题．
练习册系列答案
相关题目
6．若实数x，y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$，则z=$\sqrt{{x}^{2}+{y}^{2}}$的最大值是（ ）
| A． | $\sqrt{43}$ | B． | $\frac{5\sqrt{2}}{2}$ | C． | $\sqrt{73}$ | D． | 3$\sqrt{2}$ |
7．设数列{an}满足：a1=1，a2=3，且2nan=（n-1）an-1+（n+1）an+1，则a20的值是（ ）
| A． | 4$\frac{1}{5}$ | B． | 4$\frac{2}{5}$ | C． | 4$\frac{3}{5}$ | D． | 4$\frac{4}{5}$ |
4．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=-x2+ax-1-a，若函数f（x）为R上的单调减函数，则a的取值范围是 （ ）
| A． | a≥-1 | B． | -1≤a≤0 | C． | a≤0 | D． | a≤-1 |
12．设i是虚数单位，复数$\frac{4i}{1+i}$=（ ）
| A． | 2-2i | B． | -2-2i | C． | -2+2i | D． | 2+2i |
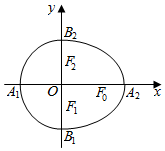我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（x≥0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$（x≤0）合成的曲线称作“果圆”，其中a2=b2+c2，a＞0，b＞c＞0．如图，点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2分别是“果圆”与x，y轴的交点．