题目内容
2.设全集U=R,集合P={x||x|>2},Q={x|x2-4x+3<0},则P∩Q=(2,3),(∁UP)∩Q=(1,2].分析 先化简集合P、Q,再求P∩Q和∁UP、(∁UP)∩Q.
解答 解:∵全集U=R,
集合P={x||x|>2}={x|x<-2或x>2}=(-∞,-2)∪(2,+∞),
Q={x|x2-4x+3<0}={x|1<x<3}=(1,3),
∴P∩Q=(2,3),
又∁UP=[-2,2],
∴(∁UP)∩Q=(1,2].
故答案为:(2,3);(1,2].
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
12.设i是虚数单位,复数$\frac{4i}{1+i}$=( )
| A. | 2-2i | B. | -2-2i | C. | -2+2i | D. | 2+2i |
17.已知集合U=R,函数$y=\sqrt{1-x}$的定义域为M,集合N={x|x2-x≤0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
14.已知直线a?平面α,直线b?平面β,α⊥β,则“a⊥b”是“a⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
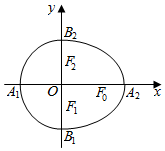 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.