题目内容
8.椭圆x2+$\frac{{y}^{2}}{4}$=1短轴的左右两个端点分别为A,B,直线l过定点(0,1)交椭圆于两点C,D.设直线AD,CB的斜率分别为k1,k2,若k1:k2=2:1,则直线l斜率k的值为( )| A. | k=2 | B. | k=3 | C. | .k=$\frac{1}{3}$或3 | D. | k=2或$\frac{1}{2}$ |
分析 求得AMB的坐标,设C(x1,y1),D(x2,y2),直线l:y=kx+1,运用直线的斜率公式,可得$\frac{{y}_{2}({x}_{1}-1)}{{y}_{1}({x}_{2}+1)}$=2,由题设知y12=4(1-x12),y22=4(1-x22),由此推出3x1x2+5(x1+x2)+3=0,所以3k2-10k+3=0,由此可推导出k的值.
解答 解:由题意可得A(-1,0),B(1,0),
设C(x1,y1),D(x2,y2),直线l:y=kx+1,
代入椭圆方程得(4+k2)x2+2kx-3=0,
△=4k2+12(4+k2)=16k2+48,
x1+x2=-$\frac{2k}{4+{k}^{2}}$,x1x2=-$\frac{3}{4+{k}^{2}}$,
k1=$\frac{{y}_{2}}{{x}_{2}+1}$,k2=$\frac{{y}_{1}}{{x}_{1}-1}$,k1:k2=2:1,
所以$\frac{{y}_{2}({x}_{1}-1)}{{y}_{1}({x}_{2}+1)}$=2,
平方,结合x12+$\frac{{{y}_{1}}^{2}}{4}$=1,所以y12=4(1-x12),
同理y22=4(1-x22),代入上式,
计算得$\frac{(1-{x}_{1})(1-{x}_{2})}{(1+{x}_{1})(1+{x}_{2})}$=4,即3x1x2+5(x1+x2)+3=0,
所以3k2-10k+3=0,解得k=3或k=$\frac{1}{3}$,
因为$\frac{{y}_{2}({x}_{1}-1)}{{y}_{1}({x}_{2}+1)}$=2,x1,x2∈(-1,1),
所以y1,y2异号,故舍去k=$\frac{1}{3}$,
所以k=3.
故选:B.
点评 本题考查椭圆的方程和性质,同时考查直线的斜率公式的运用,考查化简整理的运算能力,属于中档题.


| A. | 8 | B. | 9 | C. | 10 | D. | 7 |
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
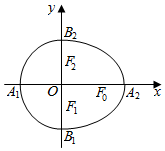 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.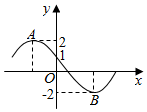 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.