题目内容
16.数列{an}中,a1=$\frac{2}{3}$,an+1=$\frac{2{a}_{n}}{{a}_{n}+1}$(1)求证:数列{$\frac{1}{{a}_{n}}-1$}是等比数列
(2)记bn=$\frac{{a}_{n}{a}_{n+1}}{{2}^{n+1}}$,数列{bn}前n项的和为Sn,求证:Sn<$\frac{1}{3}$
(3)是否存在成等差数列且互不相等的三个正整数m、s、r,使得am-1、as-1、ar-1成等比数列,若存在,求出所有满足条件的正整数m、s、r,若不存在,说明理由.
分析 (1)由条件两边取倒数,再由等比数列的定义即可得证;
(2)运用等比数列的通项公式可得an=$\frac{{2}^{n}}{1+{2}^{n}}$,求得bn=$\frac{{a}_{n}{a}_{n+1}}{{2}^{n+1}}$=$\frac{{2}^{n}}{(1+{2}^{n})(1+{2}^{n+1})}$=$\frac{1}{1+{2}^{n}}$-$\frac{1}{1+{2}^{n+1}}$,再由数列的求和方法:裂项相消求和,即可得证;
(3)假设存在互不相等的正整数m,s,r满足条件,则有$\left\{\begin{array}{l}{m+r=2s}\\{({a}_{s}-1)^{2}=({a}_{m}-1)({a}_{r}-1)}\end{array}\right.$,化简整理,再由基本不等式即可判断.
解答 解:(1)证明:由an+1=$\frac{2{a}_{n}}{{a}_{n}+1}$,可得
$\frac{1}{{a}_{n+1}}$=$\frac{1}{2}$+$\frac{1}{2{a}_{n}}$,即有$\frac{1}{{a}_{n+1}}$-1=$\frac{1}{2{a}_{n}}$-$\frac{1}{2}$,
即为$\frac{1}{{a}_{n+1}}$-1=$\frac{1}{2}$($\frac{1}{{a}_{n}}$-1),
则数列{$\frac{1}{{a}_{n}}-1$}是首项为$\frac{1}{{a}_{1}}$-1=$\frac{1}{2}$,公比为$\frac{1}{2}$的等比数列;
(2)证明:由(1)可得,$\frac{1}{{a}_{n}}-1$=($\frac{1}{2}$)n,
即有an=$\frac{{2}^{n}}{1+{2}^{n}}$,
则bn=$\frac{{a}_{n}{a}_{n+1}}{{2}^{n+1}}$=$\frac{{2}^{n}}{(1+{2}^{n})(1+{2}^{n+1})}$=$\frac{1}{1+{2}^{n}}$-$\frac{1}{1+{2}^{n+1}}$,
即有前n项的和为Sn=$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{9}$+…+$\frac{1}{1+{2}^{n}}$-$\frac{1}{1+{2}^{n+1}}$
=$\frac{1}{3}$-$\frac{1}{1+{2}^{n+1}}$<$\frac{1}{3}$.
即有Sn<$\frac{1}{3}$;
(3)由(2)知,an=$\frac{{2}^{n}}{1+{2}^{n}}$,
假设存在互不相等的正整数m,s,r满足条件,
则有$\left\{\begin{array}{l}{m+r=2s}\\{({a}_{s}-1)^{2}=({a}_{m}-1)({a}_{r}-1)}\end{array}\right.$,
可得$\frac{1}{(1+{2}^{s})^{2}}$=$\frac{1}{1+{2}^{m}}$•$\frac{1}{1+{2}^{r}}$,
化简可得1+22s+2s+1=1+2m+r+2m+2r,
即为2s+1=2m+2r,
由2m+2r≥2$\sqrt{{2}^{m}•{2}^{r}}$=2$\sqrt{{2}^{m+r}}$=2•2s=2s+1,
当且仅当m=r时等号成立,
这与m,s,r互不相等矛盾.
所以不存在互不相等的正整数m,s,r满足条件.
点评 本题考查等比数列的定义和通项公式的运用,考查构造法的运用,以及数列的求和方法:裂项相消求和,存在性问题的解法,属于中档题.

| A. | 函数y=sinx•cosx的最大值为1 | |
| B. | 将y=sin(2x+$\frac{π}{4}$)图象向右平移$\frac{π}{8}$个单位,再将所得图象上各点的横坐标变为原来的2倍,得到正弦函数y=sinx的图象 | |
| C. | 函数f(x)=1-$\frac{1}{x}$在(-∞,0)上是减函数 | |
| D. | 函数f(x)=$\frac{1}{x}$-x的图象关于y轴对称 |
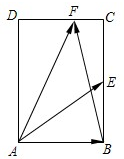
| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | 1 |
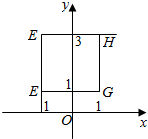
| A. | 点H(1,3)和点F(-1,1) | B. | 线段EF和线段GH | C. | 线段EH和线段FG | D. | 线段EF和线段EH |
| A. | x+$\sqrt{2}$y=4 | B. | $\sqrt{2}$x+y=3 | C. | $\sqrt{2}$x+y=4 | D. | x+$\sqrt{2}$y=2 |