题目内容
10.已知{an}是等差数列,满足a1=2,a4=14,数列{bn}满足b1=4,b4=30,且数列{bn-an}是等比数列.(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和Sn.
分析 (1)根据等差数列通项公式,求得d=4,写出等差数列{an}通项公式,{bn-an}(n∈N+)是等比数列,得得q3=8,求得q,
(2))由(1)知${b_n}=4n-2+{2^n}$(n=1,2,3…),分组求和
数列{4n-2}的前n项和为2n2,数列{2n}的前n项和为$\frac{{2×(1-{2^n})}}{1-2}={2^{n+1}}-2$即可.
解答 解:(1)设等差数列{an}的公差为d,由题意得$d=\frac{{{a_4}-{a_1}}}{3}=\frac{14-2}{3}=4$,…(1分)
所以an=a1+(n-1)d=4n-2.…(3分)
设等比数列(bn-an}的公比为q,由题意得${q^3}=\frac{{{b_4}-{a_4}}}{{{b_1}-{a_1}}}=\frac{30-14}{4-2}=8$,
解得q=2.…(4分)
所以${b_n}-{a_n}=({b_1}-{a_1}){q^{n-1}}={2^n}$,所以${b_n}=4n-2+{2^n}$(n=1,2,3…)…(6分)
(2)由(1)知${b_n}=4n-2+{2^n}$(n=1,2,3…).
数列{4n-2}的前n项和为2n2,…(7分)
数列{2n}的前n项和为$\frac{{2×(1-{2^n})}}{1-2}={2^{n+1}}-2$.…(9分)
所以,数列{bn}的前n项和为Sn=2n2+2n+1-2.…(10分)
点评 本题考查了等差数列等比数列的通项公式及其前n项和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,已知点P(0,$\frac{3}{2}$)到椭圆上的点的最远距离是$\frac{7}{4}$,则短半轴之长b=( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
20.以下关于函数f(x)=sin2x-cos2x的命题,正确的是( )
| A. | 函数f(x)在区间$(0,\frac{2}{3}π)$上单调递增 | |
| B. | 直线$x=\frac{π}{8}$是函数y=f(x)图象的一条对称轴 | |
| C. | 点$(\frac{π}{4},0)$是函数y=f(x)图象的一个对称中心 | |
| D. | 将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到$y=\sqrt{2}sin2x$的图象 |
 如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.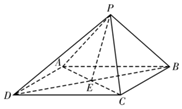 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.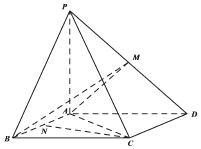 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.