题目内容
设[x],[y]分别表示不大于x,y的最大整数,如[1.6]=1,[-0.3]=-1.则集合S={(x,y)|[x]2+[y]2≤1}表示的平面区域的面积为 .
考点:二元一次不等式(组)与平面区域
专题:新定义
分析:根据[x],[y]的定义,分别讨论x,y的取值范围,即可得到对应的平面区域,然后求面积即可.
解答:
解:当0≤x<1,0≤y<1时,[x]=0,[y]=0,满足条件[x]2+[y]2≤1;
当0≤x<1,1≤y<2时,[x]=0,[y]=1,满足条件[x]2+[y]2≤1;
当0≤x<1,-1≤y<0时,[x]=0,[y]=-1,满足条件[x]2+[y]2≤1;
当-1≤x<0,0≤y<1时,[x]=-1,[y]=0满足条件[x]2+[y]2≤1;
当0≤y<1,1≤x<2时,[x]=0,[y]=1满足条件[x]2+[y]2≤1;
∴满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域是五个边长为1的正方形,其面积为:5,
故答案为:5.

当0≤x<1,1≤y<2时,[x]=0,[y]=1,满足条件[x]2+[y]2≤1;
当0≤x<1,-1≤y<0时,[x]=0,[y]=-1,满足条件[x]2+[y]2≤1;
当-1≤x<0,0≤y<1时,[x]=-1,[y]=0满足条件[x]2+[y]2≤1;
当0≤y<1,1≤x<2时,[x]=0,[y]=1满足条件[x]2+[y]2≤1;
∴满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域是五个边长为1的正方形,其面积为:5,
故答案为:5.
点评:本题主要考查区域面积的计算,根据函数的新定义,确定平面区域是解决本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
下列四个函数中,以π为最小正周期,且在区间(
,π)上为减函数的是( )
| π |
| 2 |
| A、y=2|sinx| |
| B、y=sin2x |
| C、y=2|cosx| |
| D、y=cos2x |
已知区域M:x2+y2≤4,区域N:-x≤y≤x,随机向区域M中投放一点.该点落在区域N内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 某校从高二年级学生中随机抽取40名学生,将他们的单元测试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的单元测试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.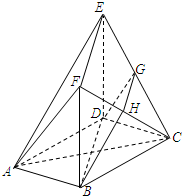 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.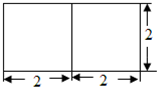 已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为
已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为