题目内容
已知函数y=
(a<0且a为常数)在区间(-∞,1]上有意义,求实数a的值.
|
考点:函数的定义域及其求法
专题:函数的性质及应用,不等式的解法及应用
分析:把函数y=
(a<0且a为常数)在区间(-∞,1]上有意义,转化为
+1≥0对任意x∈(-∞,1]恒成立,整理后分离变量求得a的范围.
|
| x |
| a |
解答:
解:∵函数y=
(a<0且a为常数)在区间(-∞,1]上有意义,
∴
+1≥0对任意x∈(-∞,1]恒成立,
即
≥0对任意x∈(-∞,1]恒成立,
又a<0,
∴x+a≤0对任意x∈(-∞,1]恒成立,
即a≤-x对任意x∈(-∞,1]恒成立,
∴a≤-1.
|
∴
| x |
| a |
即
| x+a |
| a |
又a<0,
∴x+a≤0对任意x∈(-∞,1]恒成立,
即a≤-x对任意x∈(-∞,1]恒成立,
∴a≤-1.
点评:本题考查了函数的定义域及其求法,考查了数学转化思想方法,训练了分离变量法求参数的取值范围,是中档题.

练习册系列答案
相关题目
某单位有老年人28人,中年人44人,青年人72人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
| A、简单随机抽样 |
| B、系统抽样 |
| C、分层抽样 |
| D、先从老年人中剔除一人,然后分层抽样 |
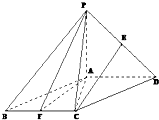 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=