题目内容
已知E,F为圆O:x2+y2=9一直径的两个端点,D为直线x-y+6=0上一动点,则
•
的最小值为 .
| DE |
| DF |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据题意画出图形,可设动点D的坐标为(x,x+6),得到
•
=2x2+12x+27=2(x+3)2+9≥9,问题得以解决.
| DE |
| DF |
解答:
解:如图所示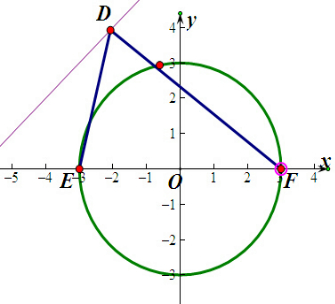 ,
,
∵E,F为圆O:x2+y2=9一直径的两个端点,
∴E的坐标为(-3,0),F的坐标为(3,0),
D为直线x-y+6=0上一动点,可设动点D的坐标为(x,x+6),
∴
=(-3-x,-x-6),
=(3-x,-x-6),
∴
•
=2x2+12x+27=2(x+3)2+9≥9,当x=-3时取等号.
∴
•
的最小值为9,
故答案为:9.
 ,
,∵E,F为圆O:x2+y2=9一直径的两个端点,
∴E的坐标为(-3,0),F的坐标为(3,0),
D为直线x-y+6=0上一动点,可设动点D的坐标为(x,x+6),
∴
| DE |
| DF |
∴
| DE |
| DF |
∴
| DE |
| DF |
故答案为:9.
点评:本题考查的知识点是平面向量的数量积的运算,直线与圆的关系性质,考虑到本题是一个填空题,我们可以用特殊值法,解答本题.

练习册系列答案
相关题目