题目内容
7.不等式2x2-axy+y2≥0对于任意x∈[1,2]及y∈[1,3]恒成立,则实数a的取值范围是( )| A. | a≤2$\sqrt{2}$ | B. | a≥2$\sqrt{2}$ | C. | a≤$\frac{11}{3}$ | D. | a≤$\frac{9}{2}$ |
分析 不等式等价变化为a≤$\frac{{2x}^{2}{+y}^{2}}{xy}$=$\frac{2x}{y}$+$\frac{y}{x}$,则求出函数$\frac{2x}{y}$+$\frac{y}{x}$的最小值即可.
解答 解:依题意,不等式2x2-axy+y2≤0等价为a≤$\frac{{2x}^{2}{+y}^{2}}{xy}$=$\frac{2x}{y}$+$\frac{y}{x}$,
设t=$\frac{y}{x}$,
∵x∈[1,2]及y∈[1,3],
∴$\frac{1}{2}$≤$\frac{1}{x}$≤1,即$\frac{1}{2}$≤$\frac{y}{x}$≤3,
∴$\frac{1}{2}$≤t≤3,
则$\frac{2x}{y}$+$\frac{y}{x}$=t+$\frac{2}{t}$,
∵t+$\frac{2}{t}$≥2$\sqrt{t•\frac{2}{t}}$=2$\sqrt{2}$,
当且仅当t=$\frac{2}{t}$,即t=$\sqrt{2}$时取等号,
故选:A.
点评 本题主要考查不等式的应用,将不等式恒成立转化为求函数的最值是解决本题的关键,要求熟练掌握函数f(x)=x+$\frac{a}{x}$,a>0图象的单调性以及应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知三点(2,3),(6,5),(4,b)共线,则实数b的值为( )
| A. | 4 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
15.如图为某几何体的三视图,则该几何体的表面积为( )


| A. | 20+2π | B. | 20+3π | C. | 24+2π | D. | 24+3π |
12.某几何体的三视图如图所示,则该几何体的体积为( )
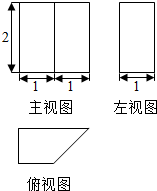

| A. | 3 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 1 |
16.一个几何体的三视图如图所示,如果该几何体的侧面面积为12π,则该几何体的体积是( )

| A. | 4π | B. | 12π | C. | 16π | D. | 48π |
17.等比数列{an}中,a5、a7是函数f(x)=x2-4x+3的两个零点,则a3•a9等于( )
| A. | -4 | B. | -3 | C. | 4 | D. | 3 |
 在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.
在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.