题目内容
2. 在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.
在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.(Ⅰ)求a1的值;
(Ⅱ)若函数y=|a1|sin($\frac{π}{4}$x+φ),|φ|<π,的一部分图象如图所示,M(-1,|a1|),N(3,-|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ-β)的值.
分析 (Ⅰ)根据等比数列和等差数列的性质进行求解即可.
(Ⅱ)根据三角函数的图象确实A,ω和φ的值即可.
解答 解:(Ⅰ) 解:由题可知${a_2}+{a_5}=18\sqrt{3}$,又a5=8a2,(3分)
故${a_2}=2\sqrt{3}$,
∴a1=$\sqrt{3}$ (5分)
(Ⅱ)∵点M(-1,|a1|),在函数y=|a1|sin($\frac{π}{4}$x+φ),|φ|<π的图象上,
∴sin(-$\frac{π}{4}$+φ)=1,
又∵|φ|<π,∴φ=$\frac{3π}{4}$ (7分)
如图,连接MN,在△MPN中,由余弦定理得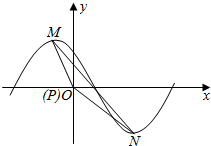
$cosβ=\frac{{{{|{PM}|}^2}+{{|{PN}|}^2}-{{|{MN}|}^2}}}{{2|{PM}||{PN}|}}=\frac{4+12-28}{{8\sqrt{3}}}=-\frac{{\sqrt{3}}}{2}$,
又∵0<β<π,∴$β=\frac{5}{6}π$(9分)
∴$ϕ-β=-\frac{π}{12}$,
∴tan(φ-β)=-tan$\frac{π}{12}$=-tan($\frac{π}{4}$-$\frac{π}{6}$)=-2+$\sqrt{3}$ (12分)
点评 本题主要考查数列与三角函数的综合,根据等比数列和等差数列的性质结合三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
13.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )


| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
10.执行如图所示的程序框图,若输出的S=945,则判断框中应填入( )


| A. | i<6? | B. | i<7? | C. | i<9? | D. | i<10? |
7.不等式2x2-axy+y2≥0对于任意x∈[1,2]及y∈[1,3]恒成立,则实数a的取值范围是( )
| A. | a≤2$\sqrt{2}$ | B. | a≥2$\sqrt{2}$ | C. | a≤$\frac{11}{3}$ | D. | a≤$\frac{9}{2}$ |
14.下列说法正确的是( )
| A. | 抛一枚硬币10次,一定有5次正面向上 | |
| B. | 明天本地降水概率为70%,是指本地下雨的面积是70% | |
| C. | 互斥事件一定是对立事件,对立事件不一定是互斥事件 | |
| D. | 若A与B为互斥事件,则P(A)+P(B)≤1 |