题目内容
19.求函数f(x)=x2e2x单调区间及极值.分析 对函数f(x)求导后,由导函数的正负来确定原函数的单调性及极值.
解答 解:f′(x)=2x•e2x+2x2•e2x
=2xe2x(1+x).
令f′(x)=0.得 x=0 或 x=-1.
当x∈(-∞,-1)时,f′(x)>0,f(x)单调递增,
当x∈(-1,0)时,f′(x)<0,f(x)单调递减,
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增,
∴f(x)的极小值为f(0)=0,极大值为f(-1)=e-2x.
f(x)的单调递增区间是(-∞,-1)和(0,+∞),
单调递减区间是(-1,0)
点评 本题考查函数求导公式和求导法则.属于基础题目.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.已知两条直线l1:x+(1+m)y+m-2=0,l2:3mx+6y+24=0互相平行,则m的值为( )
| A. | -2或1 | B. | 2或-1 | C. | -2 | D. | 1 |
10.执行如图所示的程序框图,若输出的S=945,则判断框中应填入( )


| A. | i<6? | B. | i<7? | C. | i<9? | D. | i<10? |
7.不等式2x2-axy+y2≥0对于任意x∈[1,2]及y∈[1,3]恒成立,则实数a的取值范围是( )
| A. | a≤2$\sqrt{2}$ | B. | a≥2$\sqrt{2}$ | C. | a≤$\frac{11}{3}$ | D. | a≤$\frac{9}{2}$ |
14.下列说法正确的是( )
| A. | 抛一枚硬币10次,一定有5次正面向上 | |
| B. | 明天本地降水概率为70%,是指本地下雨的面积是70% | |
| C. | 互斥事件一定是对立事件,对立事件不一定是互斥事件 | |
| D. | 若A与B为互斥事件,则P(A)+P(B)≤1 |
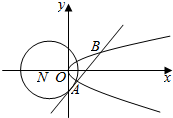 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.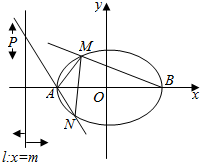 已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.
已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.