题目内容
已知函数y=f（x）满足f（x+2）=f（x-2），证明：f（x）的周期为4．
考点：函数的周期性
专题：函数的性质及应用
分析：在等式f（x+2）=f（x-2）中以x+2替换x可得f（x+4）=f（x），从而得到函数的周期．
解答：
证明：由f（x+2）=f（x-2），得f（x+2+2）=f（x+2-2）=f（x），
即f（x+4）=f（x）．
∴f（x）的周期为4．
即f（x+4）=f（x）．
∴f（x）的周期为4．
点评：本题考查了周期函数的定义，考查了函数周期的求法，是基础题．
练习册系列答案
相关题目
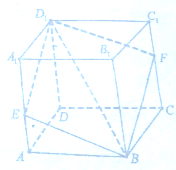如图，在棱长为1的正方体ABCD-A1B1C1D1中，过对角线BD1的平面分别交AA1，CC1于点E，F．函数f（x）=
+lg（3x+1）的定义域为（ ）
| 2x2 | ||
|
A、（-
| ||||
B、（-
| ||||
C、（-
| ||||
D、（-∞，
|
如图所示，A，B，C，D是圆O上的四个点，DE为圆O的切线，AC∥DE，直线AC与BD交于点F，若AB=2，AD=3，BD=4，则CF=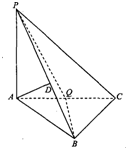
在三棱锥P-ABC中，PA⊥底面ABC，AD⊥平面PBC，其垂足D落在直线PB上，在R上定义运算?：x?y=（1-x）y，若对任意x＞2，不等式x?（x-m）≤m+2都成立，则实数m的取值范围是（ ）
| A、[-1，7] |
| B、（-∞，7] |
| C、（-∞，3] |
| D、（-∞，-1]∪[7，+∞） |
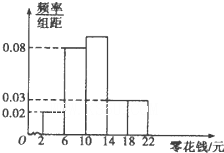一所中学共有4000名学生，为了引导学生树立正确的消费观，需抽样调查学生每天使用零花钱的数量（取整数元）情况，分层抽取容量为300的样本，作出频率分布直方图如图所示，请估计在全校所有学生中，一天使用零花钱在6元～14元的学生大约有