题目内容
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 由题意可设F(c,0),MF⊥x轴,可设M(c,n),n>0,设x=c,代入双曲线的方程,可得M的坐标,圆的半径,运用弦长公式,可得|PQ|=2$\sqrt{\frac{{b}^{4}}{{a}^{2}}-{c}^{2}}$,再由等边三角形的性质,可得a,c的方程,运用离心率公式计算即可得到所求值.
解答 解:由题意可设F(c,0),
MF⊥x轴,可设M(c,n),n>0,
设x=c,代入双曲线的方程可得y=b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=$\frac{{b}^{2}}{a}$,
即有M(c,$\frac{{b}^{2}}{a}$),
可得圆的圆心为M,半径为$\frac{{b}^{2}}{a}$,
即有M到y轴的距离为c,
可得|PQ|=2$\sqrt{\frac{{b}^{4}}{{a}^{2}}-{c}^{2}}$,
由△MPQ为等边三角形,可得
c=$\frac{\sqrt{3}}{2}$•2$\sqrt{\frac{{b}^{4}}{{a}^{2}}-{c}^{2}}$,
化简可得3b4=4a2c2,
由c2=a2+b2,可得3c4-10c2a2+3a4=0,
由e=$\frac{c}{a}$,可得3e4-10e2+3=0,
解得e2=3($\frac{1}{3}$舍去),
即有e=$\sqrt{3}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用直线和圆相交的弦长公式,考查化简整理的运算能力,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
15.命题“?x∈[1,2],x2-3x+2≤0”的否定是( )
| A. | ?x∈[1,2],x2-3x+2>0 | B. | ?x∉[1,2],x2-3x+2>0 | ||
| C. | $?{x_0}∈[{1,2}],{x_0}^2-3{x_0}+2>0$ | D. | $?{x_0}∉[{1,2}],{x_0}^2-3{x_0}+2>0$ |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,若B=$\frac{π}{2}$,a=$\sqrt{6}$,sin2B=2sinAsinC,则△ABC的面积S△ABC=( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | 6 |
9.已知集合A={x||x-1|≤2},B={x|x=2n-1,n∈Z},则A∩B=( )
| A. | {1,3} | B. | {0,2} | C. | {1} | D. | {-1,1,3} |
16.已知数列{an}为等差数列,且a1≥1,a2≤5,a5≥8,设数列{an}的前n项和为Sn,S15的最大值为M,最小值为m,则M+m=( )
| A. | 500 | B. | 600 | C. | 700 | D. | 800 |
14.已知抛物线y2=2px(p>0)的焦点为F,过点M(p,0)的直线交抛物线于A,B两点,若$\overrightarrow{AM}$=2$\overrightarrow{MB}$,则$\frac{|AF|}{|BF|}$=( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\sqrt{2}$ | D. | 与p有关 |
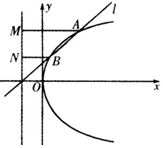 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是$\frac{2}{3}\sqrt{2}$.
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是$\frac{2}{3}\sqrt{2}$.