题目内容
12.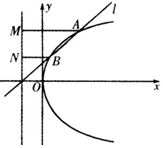 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是$\frac{2}{3}\sqrt{2}$.
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是$\frac{2}{3}\sqrt{2}$.
分析 直线y=k(x+1)(k>0)恒过定点P(-1,0),由此推导出|OB|=$\frac{1}{2}$|AF|,由此能求出点B的坐标,从而能求出k的值.
解答 解:设抛物线C:y2=4x的准线为l:x=-1
直线y=k(x+1)(k>0)恒过定点P(-1,0)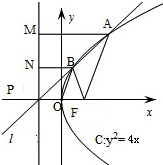
如图过A、B分别作AM⊥l于M,BN⊥l于N,
由|FA|=2|FB|,则|AM|=2|BN|,
点B为AP的中点、连接OB,
则|OB|=$\frac{1}{2}$|AF|,
∴|OB|=|BF|,点B的横坐标为$\frac{1}{2}$,
∴点B的坐标为B($\frac{1}{2}$,$\sqrt{2}$),
把B($\frac{1}{2}$,$\sqrt{2}$)代入直线l:y=k(x+1)(k>0),
解得k=$\frac{2}{3}\sqrt{2}$.
故答案为$\frac{2}{3}\sqrt{2}$.
点评 本题考查直线与圆锥曲线中参数的求法,考查抛物线的性质,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
2. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )| A. | ①③ | B. | ②③ | C. | ①④ | D. | ①③④ |
20.已知等差数列{an}满足:a2=2,Sn-Sn-3=54(n>3),Sn=100,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
7.某几何体的三视图如图所示,在该几何体的体积是( )
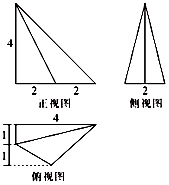

| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )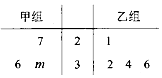

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
1.已知数列{an}、{bn}、{cn},以下两个命题:
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题 | D. | ①是假命题,②是真命题 |
2.设P={x|x<4},Q={x|x2<4},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |