题目内容
16.已知数列{an}为等差数列,且a1≥1,a2≤5,a5≥8,设数列{an}的前n项和为Sn,S15的最大值为M,最小值为m,则M+m=( )| A. | 500 | B. | 600 | C. | 700 | D. | 800 |
分析 利用已知条件求出公差的最大值以及公差的最小值,即可求解S15的最大值为M,最小值为m推出结果.
解答 解:数列{an}为等差数列,且a1≥1,a2≤5,a5≥8,设数列{an}的前n项和为Sn,S15的最大值为M,最小值为m,
可知公差最大值时,M最大,公差最小时,m最小,
可得a1=1,a2=5,此时公差d=4是最大值,
M=S15=1×15+$\frac{15×14}{2}×4$=435,a2=5,a5=8,此时d=1,
m=S15=4×15$+\frac{15×14}{2}×1$=165.
M+m=435+165=600.
故选:B.
点评 本题考查等差数列的性质的应用,考查转化思想以及计算能力,判断数列和何时取得最值是解题的关键.

练习册系列答案
相关题目
6.如图为某几何体的三视图,则该几何体的外接球的直径为( )
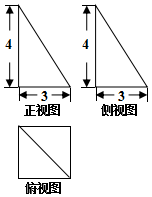

| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
7.某几何体的三视图如图所示,在该几何体的体积是( )
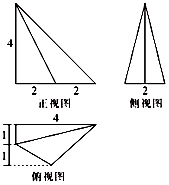

| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
11.已知两条直线m,n和两个不同平面α,β,满足α⊥β,α∩β=l,m∥α,n⊥β,则( )
| A. | m∥n | B. | m⊥n | C. | m∥l | D. | n⊥l |
1.已知数列{an}、{bn}、{cn},以下两个命题:
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题 | D. | ①是假命题,②是真命题 |
8.已知a,b,c,d都是常数,a>b,c>d,若f(x)=2017-(x-a)(x-b)的零点为c,d,则下列不等式正确的是( )
| A. | a>c>b>d | B. | a>b>c>d | C. | c>d>a>b | D. | c>a>b>d |
5.已知复数$z=\frac{a+i}{1-i}$(其中i为虚数单位),若z为纯虚数,则实数a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |
6.已知定义在R上的函数f(x)=sinωx(ω>0)的图象与x轴的两个相邻交点的距离等于$\frac{π}{2}$,若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则使y=g(x)是减函数的区间为( )
| A. | $({\frac{π}{4},\frac{π}{3}})$ | B. | $({-\frac{π}{4},\frac{π}{4}})$ | C. | $({0,\frac{π}{3}})$ | D. | $({-\frac{π}{3},0})$ |