题目内容
20.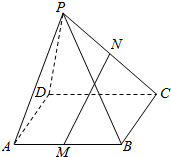 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.(1)求证:MN∥平面PAD.
(2)求异面直线MN与AD夹角的余弦值.
分析 (1)取CD中点O,连结NO、MO,推导出平面MON∥平面ADP,由此能证明MN∥平面APD.
(2)取PD中点H,连结AH、NH、AH,推导出∠HAD是异面直线MN与AD夹角,由此能求出异面直线MN与AD夹角的余弦值.
解答 证明:(1)取CD中点O,连结NO、MO,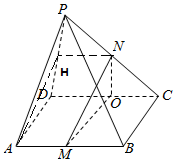
∵M、N分别是AB,PC的中点,
∴NO∥PD,MO∥AD,
∵NO∩MO=O,PD∩AD=D,
NO,MO?平面MNO,PD、AD?平面APD,
∴平面MON∥平面ADP,
∵MN?平面MON,∴MN∥平面APD.
解:(2)取PD中点H,连结AH、NH、AH,
∵O是CD中点,四边形ABCD是平行四边形,M、N分别是AB,PC的中点.
∴NH$\underset{∥}{=}$DO$\underset{∥}{=}$AM,∴四边形AMNH是平行四边形,
∴AH∥MN,∴∠HAD是异面直线MN与AD夹角,
∵三角形ADP中AD=AP=5,PD=6,∴DH=3,
∴cos$∠ADP=\frac{A{D}^{2}+P{D}^{2}-A{P}^{2}}{2×AD×PD}$=$\frac{25+36-25}{2×5×6}$=$\frac{3}{5}$,
∴cos$∠ADH=\frac{A{D}^{2}+D{H}^{2}-A{H}^{2}}{2×AD×DH}$=$\frac{25+9-A{H}^{2}}{2×5×3}$=$\frac{3}{5}$,解得AH=4,
∴cos∠HAD=$\frac{A{H}^{2}+A{D}^{2}-H{D}^{2}}{2×AH×AD}$=$\frac{16+25-9}{2×4×5}$=$\frac{4}{5}$.
∴异面直线MN与AD夹角的余弦值为$\frac{4}{5}$.
点评 本题考查线面平行的证明,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
| A. | 分层抽样、分层抽样、抽签法、系统抽样 | |
| B. | 分层抽样、分层抽样、随机数法、系统抽样 | |
| C. | 抽签法、分层抽样、随机数法、系统抽样 | |
| D. | 抽签法、分层抽样、系统抽样、随机数法 |
| A. | $\frac{\sqrt{13}}{2}$S | B. | $\frac{3}{2}$S | C. | S | D. | $\frac{1}{2}$S |