题目内容
7.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有且仅有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 化圆的一般式方程为标准方程,求出圆的圆心坐标和半径,由圆心距等于半径和可得两圆外切,数形结合可得两圆公切线的条数.>
解答 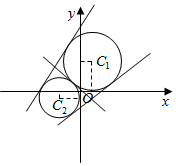 解:圆C1:x2+y2-2x-6y+1=0化为(x-1)2+(y-3)2=9,
解:圆C1:x2+y2-2x-6y+1=0化为(x-1)2+(y-3)2=9,
圆心C1(1,3),半径为r1=3,
圆C2:x2+y2+4x+2y+1=0化为(x+2)2+(y+1)2=4,
圆心C2(-2,-1),半径r2=2,
∵|C1C2|=$\sqrt{(-2-1)^{2}+(-1-3)^{2}}=5={r}_{1}+{r}_{2}$,
∴两圆外切,作出两圆图象如图,
∴圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有且仅有3条.
故选:C.
点评 本题考查圆与圆的位置关系及其判断,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
17.椭圆$\frac{{x}^{2}}{16}$+y2=1的长轴长为( )
| A. | 16 | B. | 2 | C. | 8 | D. | 4 |
2.执行如图所示的程序框图,若输入A的值为2.5,则输出的P值为( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
12.△ABC的内角A、B、C的对边分别为a,b,c,且a:b:c=$\sqrt{13}$:4:3,设$\overrightarrow{m}$=$\overrightarrow{AB}$cosA,$\overrightarrow{n}$=$\overrightarrow{AC}$sinA,又△ABC的面积为S,则$\overrightarrow{m}$•$\overrightarrow{n}$=( )
| A. | $\frac{\sqrt{13}}{2}$S | B. | $\frac{3}{2}$S | C. | S | D. | $\frac{1}{2}$S |