题目内容
14.已知A是抛物线M:y2=2px(p>0)与圆C在第一象限的公共点,其中圆心C(0,4),点A到M的焦点F的距离与C的半径相等,M上一动点到其准线与到点C的距离之和的最小值等于C的直径,O为坐标原点,则直线OA被圆C所截得的弦长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{7\sqrt{2}}{6}$ | D. | $\frac{7\sqrt{2}}{3}$ |
分析 求得圆的圆心和半径,运用抛物线的定义可得A,C,F三点共线时取得最小值,且有A为CF的中点,设出A,C,F的坐标,代入抛物线的方程可得p,由抛物线的定义可得a,求得C到直线OA的距离,运用圆的弦长公式计算即可得到所求值.
解答 解:圆C:x2+(y-4)2=a2的圆心C(0,4),半径为a,则|AC|+|AF|=2a,
由抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,
由抛物线的定义可得动点到焦点与到点C的距离之和的最小值为2a,
可得A,C,F三点共线时取得最小值,且有A为CF的中点,
由C(0,4),F($\frac{p}{2}$,0),可得A($\frac{p}{4}$,2),
代入抛物线的方程可得,4=2p•$\frac{p}{4}$,解得p=2$\sqrt{2}$,
即有a=$\frac{p}{4}$+$\frac{p}{2}$=$\frac{3\sqrt{2}}{2}$,A($\frac{\sqrt{2}}{2}$,2),
可得C到直线OA:y=2$\sqrt{2}$x的距离为d=$\frac{丨0-4丨}{\sqrt{(2\sqrt{2})^{2}+1}}$=$\frac{4}{3}$,
可得直线OA被圆C所截得的弦长为2$\sqrt{(\frac{3\sqrt{2}}{2})^{2}-(\frac{4}{3})^{2}}$=$\frac{7\sqrt{2}}{3}$,
直线OA被圆C所截得的弦长为$\frac{7\sqrt{2}}{3}$,
故选D
点评 本题考查圆的弦长的求法,注意运用抛物线的定义和三点共线和最小,同时考查弦长公式和点到直线的距离公式的运用,属于中档题.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.已知抛物线y2=4x,过其焦点F的直线l与抛物线分别交于A、B两点(A在第一象限内),$\stackrel{→}{AF}$=3$\stackrel{→}{FB}$,过AB的中点且垂直于l的直线与x轴交于点G,则三角形ABG的面积为( )
| A. | $\frac{8\sqrt{3}}{9}$ | B. | $\frac{16\sqrt{3}}{9}$ | C. | $\frac{32\sqrt{3}}{9}$ | D. | $\frac{64\sqrt{3}}{9}$ |
2.在△ABC中,A、B、C的对边分别为a、b、c,若B=$\frac{π}{3}$,b=6,sinA-2sinC=0,则a=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 12 |
9.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥3}\\{f(x+1),x<3}\end{array}\right.$f(log23)的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
19.已知等比数列{an}为递增数列,若a1>0,且2(an+2-an)=3an+1,则数列{an}的公比q=( )
| A. | 2或$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
6.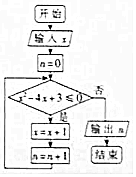 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |