题目内容
已知函数f(x)的定义域为[0,2],则g(x)=f(|x|)+f(x-
)的定义域为 .
| 1 |
| 2 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据复合函数定义域之间的关系,只要|x|、(x-
)在f(x)的定义域为[0,2]内,都即可得到结论.
| 1 |
| 2 |
解答:
解:因为函数f(x)的定义域为[0,2],
由
,解得
≤x≤2,
∴g(x)=f(|x|)+f(x-
)的定义域为[
,2];
故答案为:[
,2].
由
|
| 1 |
| 2 |
∴g(x)=f(|x|)+f(x-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题主要考查复合函数的定义域的求法,根据复合函数定义域之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设甲、乙两名射手各打了5发子弹,每发子弹击中环数如下:
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
| A、甲比乙好 | B、乙比甲好 |
| C、甲、乙一样好 | D、难以确定 |
已知a,b∈R,若a-bi=(1+i)i3(其中i为虚数单位),则( )
| A、a=1,b=1 |
| B、a=1,b=-1 |
| C、a=-1,b=1 |
| D、a=-1,b=-1 |
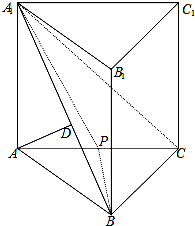 如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.