题目内容

17．在某项测量中，测量结果X服从正态分布N（1，σ2）（σ＞0），若X在（0，1）内取值的概率为0.4．则X在（0，2）内取值的概率为（　　）
A．0.8B．0.6C．0.4D．0.2

分析 根据X服从正态分布N（1，σ2），得到曲线的对称轴是直线x=1，根据所给的X在（0，1）内取值的概率为0.4，根据正态曲线的对称性知在（0，2）内取值的概率．

解答 解：∵X服从正态分布N（1，σ2）
∴曲线的对称轴是直线x=1，
∵X在（0，1）内取值的概率为0.4，
∴根据正态曲线的性质知在（0，2）内取值的概率为2×0.4=0.8．
故选：A．

点评 本题考查正态分布曲线的特点及曲线所表示的意义，主要考查正态曲线的对称性，是一个基础题，这种题目的特点是运算量小，几乎不用运算就可以得到结果．

练习册系列答案
相关题目
7．已知△ABC中，∠C=90°，AC=3，BC=4，一直线分△ABC为面积相等的两个部分，且夹在AB、BC之间的线段为MN，则MN长度的最小值为2．
8．设x，y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$，目标函数z=ax+by（a＞0，b＞0）的最大值为M，若M的取值范围是[1，2]，则点M（a，b）所在的区域是（　　）
A．B．C．D．
5．命题p：若$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-2，4），则$\overrightarrow{a}$∥$\overrightarrow{b}$；命题q：若$\overrightarrow{a}$=（1，-3），$\overrightarrow{b}$=（4，-2），λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直，则λ=1，则下列命题中真命题是（　　）
A．p∨qB．p∧qC．（￢p）∧（￢q）D．（￢p）∨q
12．如图是某几何体的三视图，则该几何体的体积是（　　）
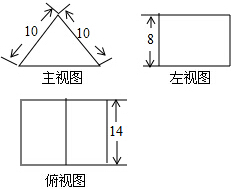
A．672B．1120C．1344D．2016
2．参数方程$\left\{\begin{array}{l}{x=cosθ（sinθ+cosθ）}\\{y=sinθ（sinθ+cosθ）}\end{array}\right.$ （θ为参数）表示什么曲线？
9．设实数x，y满足不等式组$\left\{\begin{array}{l}{x+3y-5≥0}\\{x+y≤7}\\{x-2≥0}\\{\;}\end{array}\right.$，则$\frac{y}{x}$的最大值是$\frac{5}{2}$，x+2y的最大值是12．
6．若（1-2x）6=a0+a1x+a2x+…+a6x6，则|a0|+|a1|+|a2|+…+|a6|的值为（　　）
A．1B．26C．35D．36
7．已知f（x）是定义在D上的函数，若f（x）满足：（1）对任意x∈D及任意正实数t，若x+t∈D，都有f（x+t）≥f（x）；（2）存在正实数M，使得|f（x）|≤M，则称f（x）为“单限行函数”，满足|f（x）|≤M的最小正数M叫f（x）的“单限峰值”给出下列结论：
①f（x）=2016（x∈[-1，2]）是“单限行函数”；
②f（x）=xsinx+cosx（x∈[0，$\frac{π}{2}$]）是“单限行函数”，且“单限峰值”为1；
③若f（x）=x3-12x（x∈[m，m+2]）是“单限行函数”，则-4＜m＜2；
④f（x）是定义在D上的“单限行函数”，若f（x1）=f（x2），则x1=x2
其中正确结论的个数为（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网