如图是某几何体的三视图.则该几何体的体积是( )A．672B．1120C．1344D．2016 题目和参考答案——青夏教育精英家教网—

题目内容

12．如图是某几何体的三视图，则该几何体的体积是（　　）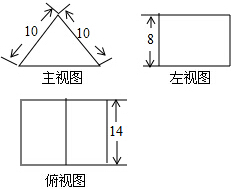

A．

672

B．

1120

C．

1344

D．

2016

分析根据几何体的三视图，得出该几何体是平放的直三棱柱，结合图中数据计算该三棱柱的体积即可．

解答解：根据几何体的三视图，得该几何体是平放的直三棱柱，
且三棱柱的底面为等腰三角形；
根据图中数据，计算该三棱柱的体积为
V=Sh=$\frac{1}{2}$×8×2$\sqrt{{10}^{2}{-8}^{2}}$×14=672．
故选：A．

点评本题考查了利用几何体的三视图求体积的应用问题，是基础题目．

练习册系列答案

	A．	向左平移$\frac{2π}{3}$个单位		B．	向右平移$\frac{2π}{3}$个单位
	C．	向左平移$\frac{π}{3}$个单位		D．	向右平移$\frac{π}{3}$个单位

3．已知函数f（x）=（m²+m）x${\;}^{{m}^{2}-2m-1}$（m∈R），分别求m的取值范围．
（1）f（x）为正比例函数；
（2）f（x）为反比例函数；
（3）f（x）在（0，+∞）上为增函数．

20．已知角α的终边过点P（-3，4），则sin α=（　　）

7．

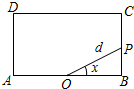如图，已知矩形ABCD中，AB=2，BC=1，O为线段AB的中点，动点P从B出发，沿矩形ABCD的边逆时针运动，运动至A点时终止．设∠BOP=x，OP=d，将d表示为x的函数d=f（x）．则下列命题中：
①f（x）有最小值1；
②f（x）有最大值$\sqrt{2}$；
③f（x）有3个极值点；
④f（x）有4个单调区间．
其中正确的是（　　）

17．在某项测量中，测量结果X服从正态分布N（1，σ²）（σ＞0），若X在（0，1）内取值的概率为0.4．则X在（0，2）内取值的概率为（　　）

4．已知等差数列{a_n}的前n项和为S_n，a₂=-2，a₈=6，则S₉=（　　）

1．已知实数x，y满足方程x²+y²-4x+1=0．
（1）求$\frac{y}{x}$的最大值与最小值；
（2）求y-x最大值与最小值；
（3）求x²+y²+2x+2y最大值与最小值；
（4）若对任意的x，y有x+2y+m≥0，求m的取值范围．

2．求下列函数的定义域：
（1）y=$\frac{3}{{2}^{x}-1}$；
（2）y=$\sqrt{{3}^{x}-81}$．

试题分类