题目内容
9.设实数x,y满足不等式组$\left\{\begin{array}{l}{x+3y-5≥0}\\{x+y≤7}\\{x-2≥0}\\{\;}\end{array}\right.$,则$\frac{y}{x}$的最大值是$\frac{5}{2}$,x+2y的最大值是12.分析 画出满足条件的平面区域,求出角点的坐标,根据$\frac{y}{x}$的几何意义求出其最大值,令z=x+2y,得:y=-$\frac{1}{2}$x+$\frac{z}{2}$,结合图象求出其最大值即可.
解答 解:画出满足条件的平面区域,如图示: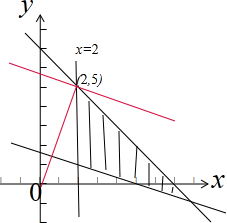 ,
,
由$\left\{\begin{array}{l}{x=2}\\{x+y=7}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,
∴$\frac{y}{x}$的最大值是$\frac{5}{2}$,
令z=x+2y,得:y=-$\frac{1}{2}$x+$\frac{z}{2}$,
结合图象得:直线过(2,5)时,z最大,z的最大值是12,
故答案为:$\frac{5}{2}$,12.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
19.若(x+1)n=xn+…+ax3+bx2+…+1(n∈N*),且a:b=3:1,则n的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
20.已知角α的终边过点P(-3,4),则sin α=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
17.在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4.则X在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.4 | D. | 0.2 |
4.已知等差数列{an}的前n项和为Sn,a2=-2,a8=6,则S9=( )
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
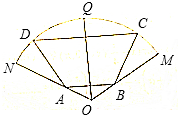 如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.
如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.