题目内容
8.设x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为M,若M的取值范围是[1,2],则点M(a,b)所在的区域是( )| A. | 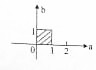 | B. | 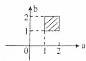 | C. |  | D. | 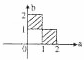 |
分析 作出可行域,变形目标函数,平移直线y=-$\frac{a}{b}$x可得1$\left\{\begin{array}{l}{1≤a≤2}\\{1≤a≤2}\end{array}\right.$,可得点(a,b)所对应的区域.
解答 解:作出约束条件所对应的可行域(如图△OAB及内部), ,
,
变形目标函数z=ax+by可得y=-$\frac{a}{b}$x+$\frac{1}{b}$z,
当-$\frac{a}{b}$≤-1时,直线经过点A(1,0)时,z取最大值a∈[1,2]
平移直线y=-$\frac{a}{b}$x可知当直线经过点A(1,0)或B(0,1)时,
目标函数取最大值M=a或M=b,由题意可得 $\left\{\begin{array}{l}{1≤a≤2}\\{1≤a≤2}\end{array}\right.$,
故选:C.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.若(x+1)n=xn+…+ax3+bx2+…+1(n∈N*),且a:b=3:1,则n的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
16.对于参数方程为$\left\{\begin{array}{l}{x=1-tcos30°}\\{y=2+tsin30°}\end{array}\right.$和$\left\{\begin{array}{l}{x=1+tcos30°}\\{y=2-tsin30°}\end{array}\right.$的曲线,正确的结论是( )
| A. | 是倾斜角为30°的平行线 | B. | 是倾斜角为30°的同一直线 | ||
| C. | 是倾斜角为150°的同一直线 | D. | 是过点(1,2)的相交直线 |
20.已知角α的终边过点P(-3,4),则sin α=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
17.在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4.则X在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.4 | D. | 0.2 |