题目内容
5.命题p:若$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,4),则$\overrightarrow{a}$∥$\overrightarrow{b}$;命题q:若$\overrightarrow{a}$=(1,-3),$\overrightarrow{b}$=(4,-2),λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,则λ=1,则下列命题中真命题是( )| A. | p∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
分析 根据平面向量的坐标表示与运算问题,结合复合命题的真值表,即可得出正确的答案.
解答 解:∵$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,4),
∴1×4-(-2)×(-2)=0,
∴$\overrightarrow{a}$∥$\overrightarrow{b}$,∴命题p是真命题;
又$\overrightarrow{a}$=(1,-3),$\overrightarrow{b}$=(4,-2),且λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,
∴(λ$\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=0
∴(λ+4)+(-3)×(-3λ-2)=0
解得λ=-1,
∴命题q是真命题.
∴p∨q为真命题.
故选:A.
点评 本题考查了平面向量的坐标表示与运算问题,也考查了复合命题的真假性判断问题,是基础题目.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
15.将八进制数123(8)化为十进制数,结果为( )
| A. | 11 | B. | 83 | C. | 123 | D. | 564 |
16.对于参数方程为$\left\{\begin{array}{l}{x=1-tcos30°}\\{y=2+tsin30°}\end{array}\right.$和$\left\{\begin{array}{l}{x=1+tcos30°}\\{y=2-tsin30°}\end{array}\right.$的曲线,正确的结论是( )
| A. | 是倾斜角为30°的平行线 | B. | 是倾斜角为30°的同一直线 | ||
| C. | 是倾斜角为150°的同一直线 | D. | 是过点(1,2)的相交直线 |
20.已知角α的终边过点P(-3,4),则sin α=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
10.已知实数x,y满足$\left\{\begin{array}{l}{5x+2y-18≤0}\\{2x-y≥0}\\{x+y-3≥0}\end{array}\right.$,若直线kx-y+1=0经过该可行域,则实数k的最大值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
17.在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4.则X在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.4 | D. | 0.2 |
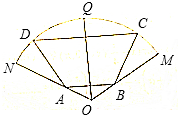 如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.
如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.