题目内容
已知c>0,且c≠1.设p:函数y=cx在上单调递减;q:函数f(x)=x2-2cx+1在(
,+∞)上为增函数.
(1)若p为真,¬q为假,求实数c的取值范围.
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
| 1 |
| 2 |
(1)若p为真,¬q为假,求实数c的取值范围.
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
考点:复合命题的真假,二次函数的性质,指数函数的单调性与特殊点
专题:
分析:利用指数函数与二次函数的单调性,分别求出p,q成立的等价条件,然后利用“p∧q”为假,“p∨q”为真,确定实数c的取值范围.
解答:
解:若p为真,
∵函数y=cx在R上单调递减,
∴0<c<1(2分)
若q为真,
∵函数f(x)=x2-2cx+1在(
,+∞)上为增函数
f(x)对称轴为x=c,
∴0<c≤
(4分)
(1)∵p为真,¬q为假,
∴实数c的取值范围是{c|0<c≤
}(6分)
(2)又“p或q”为假,“p且q”为真,
∴p真q假或p假q真,
当p真q假时,
即
<c<1
当p假q真时,
即无解
实数c的取值范围是{c|
<c<1}(12分)
∵函数y=cx在R上单调递减,
∴0<c<1(2分)
若q为真,
∵函数f(x)=x2-2cx+1在(
| 1 |
| 2 |
f(x)对称轴为x=c,
∴0<c≤
| 1 |
| 2 |
(1)∵p为真,¬q为假,
|
∴实数c的取值范围是{c|0<c≤
| 1 |
| 2 |
(2)又“p或q”为假,“p且q”为真,
∴p真q假或p假q真,
当p真q假时,
|
| 1 |
| 2 |
当p假q真时,
|
实数c的取值范围是{c|
| 1 |
| 2 |
点评:本题主要考查复合命题与简单命题之间的真假关系的应用,先求出命题p,q成立的等价条件是解决此类问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在直角坐标系中,直线y=
x+2的倾斜角是( )
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
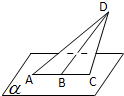 平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为
平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为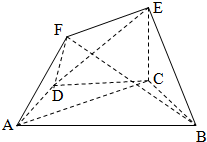 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=