题目内容

10．设四棱锥P-ABCD的底面是边长为$2\sqrt{2}$的正方形，侧棱长均为$2\sqrt{5}$，若该棱锥的五个顶点都在球O的球面上，则球O的表面积为（　　）
A．25πB．32πC．36πD．50π

分析 设AC、BD的交点为F，连接PF，则PF是四棱锥P-ABCD的高且四棱锥P-ABCD的外接球球心O在PF上．由正四棱锥的性质，结合题中数据算出AF=2且PF=4，Rt△AOF中根据勾股定理，得R2=22+（4-R）2，解之得R=2.5，利用球的表面积公式即可算出经过该棱锥五个顶点的球面面积．

解答 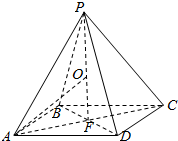解：设AC、BD的交点为F，连接PF，则PF是四棱锥P-ABCD的高，
根据球的对称性可得四棱锥P-ABCD的外接球球心O在直线PF上，
∵正方形ABCD边长为2$\sqrt{2}$，∴AF=$\frac{\sqrt{2}}{2}$AB=2
Rt△PAF中，PF=4
连接OA，设OA=0P=R，则
Rt△AOF中AO2=AF2+OF2，即R2=22+（4-R）2
解之得R=2.5
∴四棱锥P-ABCD的外接球表面积为S=4πR2=4π×2.52=25π
故选：A．

点评 本题给出正四棱锥，求它的外接球的表面积，着重考查了正四棱锥的性质、勾股定理和球的表面积公式等知识，属于基础题．

练习册系列答案
相关题目
11．函数y=cos（sinx）的奇偶性是偶函数．
1．已知⊙O：x2+y2=4（注：横、纵坐标是有理数的点称为有理点）．
①⊙O上只有四个有理点；
②⊙O上有无数个有理点；
③⊙O上只有有限个无理点；
④以⊙O上点（1，$\sqrt{3}$）为圆心，半径为4的圆上最多只有两个有理点．
以上结论正确的序号为②．
18．已知命题p：0＜a＜4，命题q：函数y=ax2-ax+1的值恒为正，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
5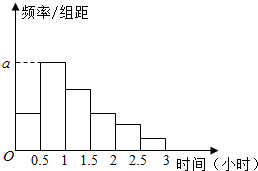．随着智能手机等电子产品的普及，“低头族”正成为现代社会的一个流行词．在路上、在餐厅里、在公交车上，随处可见低头玩手机的人，这种“低头族现象”冲击了人们面对面交流的温情，也对人们的健康构成一定的影响．为此，某报社发起一项专题调查，记者随机采访了M名市民，得到这M名市民每人在一天内低头玩手机的时间（单位：小时），根据此数据作出频数的统计表和频率分布直方图如下：
分组频数频率
[0，0.5）40.10
[0.5，1）mp
[1，1.5）10n
[1.5，2）60.15
[2，2.5）40.10
[2.5，3）20.05
合计M1
（Ⅰ）求出表中的M，p及图中a的值；
（Ⅱ）试估计这M名市民在一天内低头玩手机的平均时间（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从一天内低头玩手机的时间不少于2小时的市民中任取2人，求两人在一天内低头玩手机的时间都在区间[2，2.5）内的概率．
15．椭圆$\frac{x^2}{m}+\frac{y^2}{4}$=1的焦距为2，则m的值是（　　）
A．6或2B．5C．1或9D．3或5
2．命题“若a＞0，则a＞1”的逆命题、否命题、逆否命题这三个命题中，真命题的个数为2．
19．如图，在正三棱柱ABC-A1B1C1中，点D在边BC上，AD⊥C1D．
（1）求证：AD⊥平面BCC1B1；
（2）如果点E是C1B1的中点，求证：A1E∥平面ADC1．
20．已知F是抛物线x2=8y的焦点，若抛物线上的点A到x轴的距离为5，则|AF|=（　　）
A．4B．5C．6D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网