题目内容
19. 如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.(1)求证:AD⊥平面BCC1B1;
(2)如果点E是C1B1的中点,求证:A1E∥平面ADC1.
分析 (1)推导出AD⊥C1D,从而CC1⊥平面ABC,进而AD⊥CC1,由此能证明AD⊥平面BCC1B1.
(2)由AD⊥BC,得D是BC中点,连结ED,得四边形AA1DE是平行四边形,由此能证明A1E∥平面ADC1.
解答  证明:(1)∵在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D,
证明:(1)∵在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D,
∴CC1⊥平面ABC,又AD?平面ABC,
∴AD⊥CC1,
又C1D∩CC1=C1,∴AD⊥平面BCC1B1.
(2)∵AD⊥平面BCC1B1,∴AD⊥BC,
∵在正三棱柱ABC-A1B1C1中,AB=BC=AC,∴D是BC中点,
连结ED,∵点E是C1B1的中点,
∴AA1$\underset{∥}{=}$DE,∴四边形AA1DE是平行四边形,
∴A1E∥AD,
又A1E?面ADC1,AD?平面ADC1.
∴A1E∥平面ADC1.
点评 本题考查线面垂直的证明,考查线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
9.已知全集U={0,1,2,3,4},M={2,3,4},N={0,1,2,3},则图中阴影部分所表示的集合为( )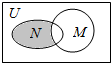

| A. | {2,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1} |
10.设四棱锥P-ABCD的底面是边长为$2\sqrt{2}$的正方形,侧棱长均为$2\sqrt{5}$,若该棱锥的五个顶点都在球O的球面上,则球O的表面积为( )
| A. | 25π | B. | 32π | C. | 36π | D. | 50π |
4.在等比数列{an}中,已知a1=1,a3=2a2,则该数列前6项和S6=( )
| A. | 31 | B. | 63 | C. | 127 | D. | 176 |
8.在[-4,4]上随机取一个实数m,能使函数f(x)=x3+mx2+3x在R上单调递增的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.