题目内容
一个袋中装有若干个大小相同的黑球、白球和红球．已知从袋中任意摸出1个球，得到黑球的概率为
；从袋中任意摸出2个球，至少得到1个白球的概率为
．
（Ⅰ）若袋中共有10个球；
（1）求白球的个数；
（2）从袋中任意摸出3个球，记得到白球的个数为ξ，求ξ的数学期望E（ξ）．
（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
．
| 2 |
| 5 |
| 7 |
| 9 |
（Ⅰ）若袋中共有10个球；
（1）求白球的个数；
（2）从袋中任意摸出3个球，记得到白球的个数为ξ，求ξ的数学期望E（ξ）．
（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
| 7 |
| 10 |
考点：离散型随机变量的期望与方差,互斥事件与对立事件
专题：概率与统计
分析：（Ⅰ）（1）记“从袋中任意摸出2个球，至少得到1个白球”为事件A，利用对立事件的概率计算公式能求出白球有5个．
（2）随机变量ξ的所有可能取值为0，1，2，3，分别求出相对应的概率，由此能求出ξ的分布列和Eξ．0×
+1×
+2×
+3×
=
．
（Ⅱ）设袋中有n个球，其中y个黑球，由题意得y=
n，由此能证明从袋中任意摸出2个球，至少得到1个黑球的概率不大于
．
（2）随机变量ξ的所有可能取值为0，1，2，3，分别求出相对应的概率，由此能求出ξ的分布列和Eξ．0×
| 1 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
| 1 |
| 12 |
| 3 |
| 2 |
（Ⅱ）设袋中有n个球，其中y个黑球，由题意得y=
| 2 |
| 5 |
| 7 |
| 10 |
解答：
（Ⅰ）解：（1）记“从袋中任意摸出2个球，至少得到1个白球”为事件A，
记袋中白球个数为x，则
P（A）=1-
=
，
解得x=5，
∴白球有5个．
（2）随机变量ξ的所有可能取值为0，1，2，3，
P（ξ=0）=
=
，
P（ξ=1）=
=
，
P（ξ=2）=
=
，
P（ξ=3）=
=
，
∴ξ的分布列为：
∴Eξ=0×
+1×
+2×
+3×
=
．
（Ⅱ）证明：设袋中有n个球，其中y个黑球，由题意得y=
n，
∴2y＜n，2y≤n-1，∴
≤
，
设“从袋中任意摸出2个球，至少得到1个黑球”为事件B，
则P（B）=
+
×
≤
+
×
=
．
记袋中白球个数为x，则
P（A）=1-
| ||
|
| 7 |
| 9 |
解得x=5，
∴白球有5个．
（2）随机变量ξ的所有可能取值为0，1，2，3，
P（ξ=0）=
| ||
|
| 1 |
| 12 |
P（ξ=1）=
| ||||
|
| 5 |
| 12 |
P（ξ=2）=
| ||||
|
| 5 |
| 12 |
P（ξ=3）=
| ||
|
| 1 |
| 12 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
| 1 |
| 12 |
| 3 |
| 2 |
（Ⅱ）证明：设袋中有n个球，其中y个黑球，由题意得y=
| 2 |
| 5 |
∴2y＜n，2y≤n-1，∴
| y |
| n-1 |
| 1 |
| 2 |
设“从袋中任意摸出2个球，至少得到1个黑球”为事件B，
则P（B）=
| 2 |
| 5 |
| 3 |
| 5 |
| y |
| n-1 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 7 |
| 10 |
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要注意排列组合知识的合理运用．
练习册系列答案
相关题目
设f（x）可导，且y=f（e2x），则y′=（ ）
| A、f′（e2x） |
| B、f′（e2x）e2x |
| C、2f′（e2x） |
| D、2f′（e2x）e2x |
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人，吴老师采用A、B两种不同的教学方式分别在甲、乙两个班进行教学实验．为了解教学效果，期末考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图所示．记成绩不低于90分者为“成绩优秀”．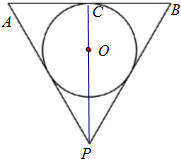
设倒圆锥形容器的轴截面为一个等边三角形，在此容器内注入水，并浸入半径为r的一个实心球，使球与水面恰好相切，试求取出球后水面高为多少？