题目内容
已知函数f(x)=
的定义域为集合A,函数g(x)=(
)x(-1≤x≤0)的值域为集合B,U=R.
(1)求(∁UA)∩B;
(2)若C={x|a≤x≤2a-1}且C⊆B,求实数a的取值范围.
| 1 | ||
|
| 1 |
| 2 |
(1)求(∁UA)∩B;
(2)若C={x|a≤x≤2a-1}且C⊆B,求实数a的取值范围.
考点:交、并、补集的混合运算,集合的包含关系判断及应用
专题:函数的性质及应用,集合
分析:(1)由函数f(x)的解析式求出定义域A,由补集的运算求出∁UA,再由指数函数的性质求出函数g(x)的值域B,再由交集的运算求出(∁UA)∩B;
(2)根据子集的定义和条件对集合B分B=∅和B≠∅两种情况,分别列出不等式组求出a的范围.
(2)根据子集的定义和条件对集合B分B=∅和B≠∅两种情况,分别列出不等式组求出a的范围.
解答:
解:(1)要是函数f(x)=
有意义,则x-1>0,得x>1,
所以函数f(x)的定义域A=(1,+∞),则∁UA=(-∞,1],
由-1≤x≤0得,1≤(
)x≤2,则函数g(x)的值域B=[1,2],
所以(∁UA)∩B={1};…(5分)
(2)因为C={x|a≤x≤2a-1}且C⊆B,
所以对集合B分B=∅和B≠∅两种情况,
则a>2a-1或
,解得a<1或1≤a≤
,
所以实数a的取值范围是(-∞,
]…(10分)
| 1 | ||
|
所以函数f(x)的定义域A=(1,+∞),则∁UA=(-∞,1],
由-1≤x≤0得,1≤(
| 1 |
| 2 |
所以(∁UA)∩B={1};…(5分)
(2)因为C={x|a≤x≤2a-1}且C⊆B,
所以对集合B分B=∅和B≠∅两种情况,
则a>2a-1或
|
| 3 |
| 2 |
所以实数a的取值范围是(-∞,
| 3 |
| 2 |
点评:本题考查补、交、并的混合运算,由集合之间的关系求出参数的范围,及指数函数的性质,属于基础题.

练习册系列答案
相关题目
f(x)是定义在R上的奇函数且x>0时,f(x)=2x2-x+3,则当x<0时,f(x)的解析式为( )
| A、2x2-x+3 |
| B、-2x2+x-3 |
| C、2x2+x+3 |
| D、-2x2-x-3 |
已知数列{an}的前n项和Sn=n2,则a4=( )
| A、-7 | B、-9 | C、7 | D、9 |
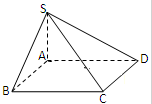 在四棱锥S-ABCD中,∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小.
在四棱锥S-ABCD中,∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小.