题目内容
20.已知集合A={2,3},则集合A的子集的个数为4.分析 根据集合之间的关系,如果A?B,那么?x∈A,都有x∈B,由此得到集合A的所有子集.
解答 解:由已知,A={2,3},它的子集有∅,{2},{3},{2,3}共有4个;
故答案为:4.
点评 本题考查了集合的子集的求法;如果一个集合有n个元素,那么它的子集有2n个,真子集有2n-1个.

练习册系列答案
相关题目
10.已知x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-3y的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 7 | D. | $-\frac{1}{2}$ |
11.函数$f(x)=-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x$的极大值点是( )
| A. | $-\frac{4}{5}$ | B. | 1 | C. | $\frac{7}{6}$ | D. | -2 |
9.设抛物线y2=2px(p>0)的焦点为F.若F到直线y=$\sqrt{3}$x的距离为$\sqrt{3}$,则p=( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
10.将函数y=cos2x的图象向左平移$\frac{π}{3}$个单位长度,所得图象的函数解析式为( )
| A. | $y=cos(2x-\frac{2π}{3})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x+\frac{2π}{3})$ | D. | $y=cos(2x-\frac{π}{3})$ |
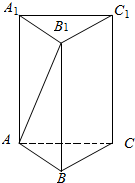 如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.
如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.