题目内容
2.下列各式中,值为$\sqrt{3}$的是( )| A. | sin15°cos15° | B. | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C. | $\frac{{1+tan{{15}^0}}}{{1-tan{{15}^0}}}$ | D. | $\sqrt{\frac{1+cos30°}{2}}$ |
分析 由条件利用二倍角公式、两角和的差三角公式,求出各个选项中式子的值,从而得出结论.
解答 解:由于sin15°cos15°=$\frac{1}{2}$sin30°=$\frac{1}{4}$,故排除A.
由于${cos}^{2}\frac{π}{12}$-${sin}^{2}\frac{π}{12}$=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,故排除B.
由于$\frac{1+tan15°}{1-tan15°}$=tan60°=$\sqrt{3}$,满足条件.
由于$\sqrt{\frac{1+cos30°}{2}}$=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
故排除D,
故选:C.
点评 本题主要二倍角公式、两角和的差三角公式,属于基础题.

练习册系列答案
相关题目
10.将函数y=cos2x的图象向左平移$\frac{π}{3}$个单位长度,所得图象的函数解析式为( )
| A. | $y=cos(2x-\frac{2π}{3})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x+\frac{2π}{3})$ | D. | $y=cos(2x-\frac{π}{3})$ |
7.若双曲线2kx2-ky2=1的一个焦点的坐标为(0,4),则k的值为( )
| A. | $\frac{3}{32}$ | B. | $\frac{16}{3}$ | C. | -$\frac{3}{32}$ | D. | -$\frac{16}{3}$ |
12.有5本不同的书,其中语文书2本,数学书2本,物理书1本,若从中任抽一本,抽到的书是数学书的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
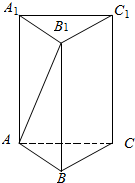 如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.
如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.