题目内容
已知函数f(x)=2
sinxcosx-sin2x+
cos2x+
,x∈R.
(1)求函数f(x)在[-
,
]上的最值;
(2)若将函数f(x)的图象向右平移
个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到g(x)的图象,已知g(α)=-
,α∈(
,
),求cos(
-
)的值.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)求函数f(x)在[-
| π |
| 4 |
| π |
| 2 |
(2)若将函数f(x)的图象向右平移
| π |
| 4 |
| 6 |
| 5 |
| 4π |
| 3 |
| 11π |
| 6 |
| α |
| 2 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用倍角公式将函数进行化简,结合三角函数的图象和性质即可求函数f(x)在[-
,
]上的最值;
(2)根据三角函数的图象关系求出g(x)的表达式,利用三角函数的关系式进行求值即可.
| π |
| 4 |
| π |
| 2 |
(2)根据三角函数的图象关系求出g(x)的表达式,利用三角函数的关系式进行求值即可.
解答:
解:(1)f(x)=2
sinxcosx-sin2x+
cos2x+
=
sin2x-
+
cos2x+
=
sin2x+cos2x=2sin(2x+
).
∵x∈[-
,
],∴-
≤2x+
≤
,
∴当2x+
=-
,即x=-
时,f(x)的最小值为2×(-
)=-
.
当2x+
=
,即x=
时,f(x)的最大值为2×1=2.
(2)若将函数f(x)的图象向右平移
个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到g(x)=2sin(x-
),
由g(α)=2sinx(α-
)=-
,
得sinx(α-
)=-
,
∵α∈(
,
),
∴π-α∈(π,
),
是cos(α-
)=-
,
∵
<
-
<
,
∴cos(
-
)=-
=-
=-
.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
∵x∈[-
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 7π |
| 6 |
∴当2x+
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| ||
| 2 |
| 3 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
(2)若将函数f(x)的图象向右平移
| π |
| 4 |
| π |
| 3 |
由g(α)=2sinx(α-
| π |
| 3 |
| 6 |
| 5 |
得sinx(α-
| π |
| 3 |
| 3 |
| 5 |
∵α∈(
| 4π |
| 3 |
| 11π |
| 6 |
∴π-α∈(π,
| 3π |
| 2 |
是cos(α-
| π |
| 3 |
| 4 |
| 5 |
∵
| π |
| 2 |
| α |
| 2 |
| π |
| 6 |
| 3π |
| 4 |
∴cos(
| α |
| 2 |
| π |
| 6 |
|
|
| ||
| 10 |
点评:本题主要考查三角函数的最值的求解,根据倍角公式将函数化简是解决本题的关键,要求熟练三角函数的图象和性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知α、β是两个不同的平面,m、n是平面α及平面β之外的两条不同直线,给出四个论断:①m∥n,②α∥β,③m⊥α,④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .
如图,已知直角三角形ACB中,∠C=90°,D为AC上一点,且
=2
,∠ABD=30°,则cos∠ADB=( )
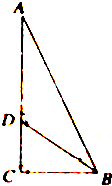
| AD |
| DC |

A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
数列{an},已知a1=2,an+1=1-
(n∈N*),则a2014等于( )
| 1 |
| an |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |