题目内容
已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且
•
=
•
,动点P的轨迹为C,已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1,|DB|=l2,则
+
的最大值为( )
| QP |
| QF |
| FP |
| FQ |
| l1 |
| l2 |
| l2 |
| l1 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、3
|
考点:基本不等式,平面向量的综合题
专题:不等式的解法及应用,圆锥曲线中的最值与范围问题
分析:如图所示,设P(x,y),则Q(x,-1),由
•
=
•
,利用数量积运算得到动点P的轨迹C为:x2=4y.设M(a,
).(a∈R).得到⊙M的方程为:(x-a)2+(y-
)2=a2+(
-2)2.令y=0,则x2-2ax+a2=4,可得A(a+2,0),B(a-2,0).利用两点之间的距离公式可得|DA|=l1,|DB|=l2.当a≠0时,
+
=
=
变形利用基本不等式即可得出.a=0,直接得出.
| QP |
| QF |
| FP |
| FQ |
| a2 |
| 4 |
| a2 |
| 4 |
| a2 |
| 4 |
| l1 |
| l2 |
| l2 |
| l1 |
| ||||
| l1l2 |
| 2a2+16 | ||
|
解答:
解:如图所示,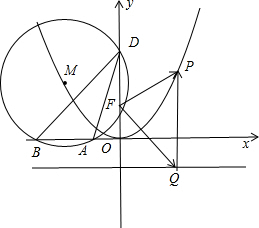
设P(x,y),则Q(x,-1),
∵
•
=
•
,
∴(0,y+1)•(-x,2)=(x,y-1)•(x,-2),
∴2(y+1)=x2-2(y-1),
化为x2=4y.
∴动点P的轨迹C为:x2=4y.
设M(a,
).(a∈R).
则⊙M的方程为:(x-a)2+(y-
)2=a2+(
-2)2.
化为x2-2ax+y2-
y=4-a2.
令y=0,则x2-2ax+a2=4,
解得x=a+2,或a-2.
取A(a+2,0),B(a-2,0).
∴|DA|=l1=
,
|DB|=l2=
.
当a≠0时,
+
=
=
=2
=2
=2
≤2
=2
,当且仅当a=±2
时取等号.
当a=0时,
+
=2.
综上可得:
+
的最大值为2
.
故选:C.

设P(x,y),则Q(x,-1),
∵
| QP |
| QF |
| FP |
| FQ |
∴(0,y+1)•(-x,2)=(x,y-1)•(x,-2),
∴2(y+1)=x2-2(y-1),
化为x2=4y.
∴动点P的轨迹C为:x2=4y.
设M(a,
| a2 |
| 4 |
则⊙M的方程为:(x-a)2+(y-
| a2 |
| 4 |
| a2 |
| 4 |
化为x2-2ax+y2-
| a2 |
| 2 |
令y=0,则x2-2ax+a2=4,
解得x=a+2,或a-2.
取A(a+2,0),B(a-2,0).
∴|DA|=l1=
| (a+2)2+4 |
|DB|=l2=
| (a-2)2+4 |
当a≠0时,
| l1 |
| l2 |
| l2 |
| l1 |
| ||||
| l1l2 |
| 2a2+16 | ||
|
|
1+
|
1+
|
1+
|
| 2 |
| 2 |
当a=0时,
| l1 |
| l2 |
| l2 |
| l1 |
综上可得:
| l1 |
| l2 |
| l2 |
| l1 |
| 2 |
故选:C.
点评:本题综合考查了数量积的运算、点的轨迹方程、两点之间的距离公式、基本不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.下列各对事件中,为对立事件的是( )
| A、恰有一名男生和恰有2名男生 |
| B、至少一名男生和至少一名女生 |
| C、至少有一名男生和与全是女生 |
| D、至少有一名男生和全是男生 |
各项都为正数的等比数列{an}中,a1=2,a3=8,则公比q的值为( )
| A、2 | B、3 | C、4 | D、5 |
 某样本数据的频率分布直方图的部分图形如图所示,则数据在[50,70)的频率约为( )
某样本数据的频率分布直方图的部分图形如图所示,则数据在[50,70)的频率约为( )| A、0.25 | B、0.5 |
| C、0.05 | D、0.025 |
由a1=1,an+1=
给出的数列{an}的第34项是( )
| an |
| 3an+1 |
A、
| ||
| B、100 | ||
C、
| ||
D、
|
已知平面向量
=(λ,-2),
=(4,1),若
∥
,则实数λ等于( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、-8 | ||
| D、8 |