题目内容
已知
=-2,则sinx的值为 .
| 1-cosx+sinx |
| 1+cosx+sinx |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式去分母,整理后表示出cosx,代入sin2x+cos2x=1中求出sinx的值即可.
解答:
解:已知等式变形得:1-cosx+sinx=-2-2cosx-2sinx,
整理得:3sinx+cosx=-3,即cosx=-3sinx-3,
代入sin2x+cos2x=1中,得:sin2x+(-3sinx-3)2=1,
整理得:5sin2x+9sinx+4=0,
即(sinx+1)(5sinx+4)=0,
解得:sinx=-1或sinx=-
,
当sinx=-1时,cosx=0,1+cosx+sinx=0,分母为0,不合题意,
则sinx=-
.
故答案为:-
整理得:3sinx+cosx=-3,即cosx=-3sinx-3,
代入sin2x+cos2x=1中,得:sin2x+(-3sinx-3)2=1,
整理得:5sin2x+9sinx+4=0,
即(sinx+1)(5sinx+4)=0,
解得:sinx=-1或sinx=-
| 4 |
| 5 |
当sinx=-1时,cosx=0,1+cosx+sinx=0,分母为0,不合题意,
则sinx=-
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
如果f(x)为定义在R上的偶函数,且导数f′(x)存在,则f′(0)的值为( )
| A、2 | B、1 | C、0 | D、-1 |
i为虚数单位,则
等于( )
| 2 |
| 1-i |
| A、1-i | B、1+i |
| C、2-2i | D、2+2i |
“m=n”是“方程mx2+ny2=1表示圆”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
椭圆
+
=1 (a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈[
,
],则椭圆的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 12 |
| 5π |
| 12 |
A、[
| ||||||||
B、(0,
| ||||||||
C、[
| ||||||||
D、[
|
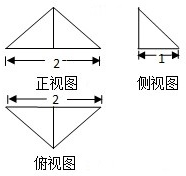 一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为
一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为